Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 119

Resolver o P r o b .   4.118 , considerando que a tensão admissível compreensiva é reduzida para 60   M p a .

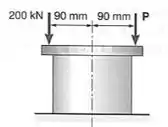
Passo 1

Sabemos que a fórmula de tensão é dada por:

σ = - F A + M y I

Tendo essas duas relações, precisamos agora começar a determinar o que temos, sendo assim podemos anotar no próximo passo.

Passo 2

Agrupando os dados que temos podemos definir que:

  • Dados da seção

    • A área da seção vai ser feita da seguinte maneira:

    A = π D e 2 4 - π D I 2 4 = π 160 2 4 - π 130 2 4 = 6833   m m 2

    E o momento de inércia é calculado pela seguinte equação:

    I = π r e 4 4 - π r I 4 4 = π 80 4 4 - π 65 4 4 = 18150061   m m 4

  • Dados de Y para determinar o cálculo das tensões.

Como queremos o intervalo em que P pode atuar, precisamos pensar em duas situações, uma em que o momento some a tensão e uma em que a tensão subtraia, sendo assim temos que:

σ A = - F A + M y A I

σ B = - F A + M y B I

Sabemos que:

F = P + 200000

M = 90   .   200000 - 90 P

σ A = - 60   M P a = - 60 N m m 2

Substituindo teremos que:

- 60 = - P + 200000 6833   - ( 90   .   200000 - 90 P ) ( 80 ) 18150061

- 60 = - P + 200000 6833   + ( 90   .   200000 - 90 P ) ( 80 ) 18150061

Sendo assim o nosso sistema será dado por:

- 60 = - P 6833   - 200000 6833   + 90 P 80 18150061 - 90   .   200000   .     80 18150061

- 60 = - P 6833   - 200000 6833   - 90 P 80 18150061 + 90   .   200000   .     80 18150061

- 60 + 200000 6833   + 90   .   200000   .   80 18150061 = - 1,46   .   10 - 4 P + 3,97   . 10 - 4 P

- 60 + 200000 6833   - 90   .   200000   .     80 18150061 = - 1,46   .   10 - 4 P - 3,97   . 10 - 4 P

- 60 + 29,3 + 79,3 = 2,51   .   10 - 4 P

- 60 + 29,3 - 79,3 = 5,43   . 10 - 4 P

+ 48,6 = 2,51   . 10 - 4 P

P = 193625   N = 194   k N

- 110 = - 5,43   .   10 - 4 P

P = 202578   N = 203   k N

Assim o intervalo de cargas é dado por:

194 < P < 203  

Resposta

194 < P < 203  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formando um ângulo β com a vertical. Determinar: (b) a tensão no ponto B .
O momento M é aplicado a uma viga de seção transversal mostrada, em um plano formando um ângulo β com a vertical. Determinar: (a) a tensão no ponto A .
O momento M atua em um plano vertical e está aplicado a uma viga orientada como mostrado. Determinar: (b) a máxima tensão de tração na viga.
O momento M atua em um plano vertical e está aplicado a uma viga orientada como mostrado. Determinar: (a) o ângulo que o eixo neutro forma com o plano horizontal.
O momento M atua em um plano vertical e está aplicado a uma viga orientada como mostrado. Determinar: (a) o ângulo que o eixo neutro forma com o plano horizontal.