Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 15
Selecione no Apêndice B a viga de aço de abas largas de mais curta e de menor peso que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é e a tensão de cisalhamento admissível é
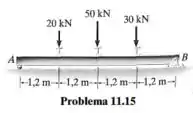
Passo 1
Começamos com as reações de apoio.
Aplicando as equações de equilíbrio:
Passo 2
Utilizando o método gráfico e a tabela 6.1 geramos os diagramas de esforço cortante e momento fletor:
O gráfico de esforço cortante é gerado diretamente utilizando a tabela, basta subtrair ou adicionar o valor das forças a medida em que o gráfico passa por elas.
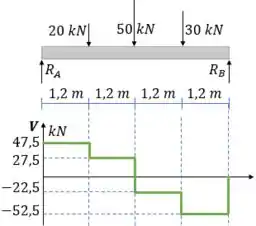
Utilizando as áreas abaixo do gráfico de esforço cortante podemos gerar o gráfico de momento fletor:
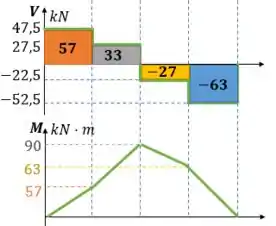
Assim encontramos os esforços máximos na viga:
Passo 3
Aplicamos a equação 11.1 para determinar a resistência necessária para a viga:
Passo 4
Observando o apêndice B encontramos a viga , contudo está é uma viga muito larga e a questão pede uma viga curta. Uma melhor opção será viga:
Com as seguintes propriedades:
Passo 5
Como esta é uma viga de abas largas, podemos utilizar a equação a seguir para testar se ela resistirá ao cisalhamento:
Como a tensão de cisalhamento admissível é de a viga selecionada é compatível com o projeto