Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 14

Selecione no Apêndice B a viga estrutural de abas largas de menor peso e menor altura que suportará com segurança as cargas mostradas na figura. A tensão de flexão admissível é σ a d m = 168   M P a e a tensão de cisalhamento admissível é τ a d m = 100   M P a

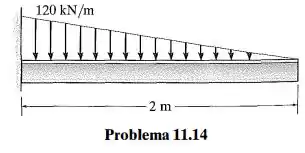
Passo 1

Vamos começar calculando as reações de apoio:

∑ M = 0 ⇒ M A - 120 ⋅ 2 2 ⋅ 2 ⋅ 1 3 = 0

M A = 80   k N m

∑ F y = 0 ⇒ R A - 120 ⋅ 2 2 = 0

R A = 120   k N

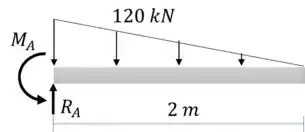
Passo 2

Em uma viga engastada com carregamento uniforme o ponto de esforço máximo é o engaste.

M m a x = 80   k N m

R A = 120   k N

Passo 3

Aplicamos a equação 11.1 para determinar a resistência necessária da viga sobre flexão

S = M m á x σ a d m

S = 80   k N ⋅ m 168   M P a

S = 476,2 ⋅ 10 3 m m 3

Baseado nisso, procuramos no apêndice B uma viga adequada:

W 310 x 39

S = 547 ⋅ 10 3   m m 3

d = 310   m m

t a l m a = 5.84   m m

Passo 4

Agora podemos testar nossa viga pra garantir que ela resista ao cisalhamento:

τ = V m á x t a l m a ⋅ d

τ = 120   k N 310   m m ⋅ 5.84   m m

τ = 66 ,   28   M P a

Como a tensão de cisalhamento admissível é τ a d m = 100   M P a , a nossa viga selecionada é capaz de resistir.

Resposta

W 310 x 39

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A polia acoplada à extremidade do eixo está sujeita à carga mostrada na figura. Se os mancais em A e B exercerem somente as componentes y e z da força sobre o eixo, determine o torque de equilíbrio T
A viga tem a forma de um tronco de cone reto com diâmetro de 0,3m em A e diâmetro de 0,6m em B . Se suportar um momento de 12k N . m em sua extremidade, determine a tensão de flexão máxima absoluta na
A polia acoplada à extremidade do eixo está sujeita à carga mostrada na figura. Se os mancais em A e B exercerem somente as componentes y e z da força sobre o eixo, determine o torque de equilíbrio T
Os mancais em A e B exercem somente as componentes x e z das forças sobre o eixo de aço. Determine, com aproximação de 1m m , o diâmetro do eixo, de modo que ele possa resistir às cargas das engrenage
A viga em balanço tem seção transversal circular. Se ela suportar uma força P em sua extremidade, determine seu raio y em função de x, de modo que seja submetida a uma tensão de flexão máxima constant