Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 9
A viga simplesmente apoiada é composta por duas seções W310x33 montadas como mostra a figura. Determine se ela suportará com segurança uma carga . A tensão de flexão admissível é o e a tensão de cisalhamento admissível for
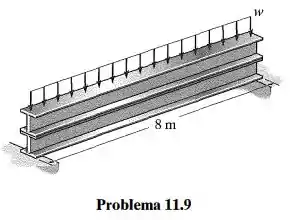
Passo 1
Dados da questão:
Dados da viga: , , ,
A questão pede:
Passo 2
Começamos com as reações de apoio:
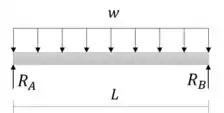
Por simetria do carregamento
Pelas equações de equilíbrio:
Passo 3
Utilizamos o método gráfico para determinar o diagrama de momento fletor e esforço cortante
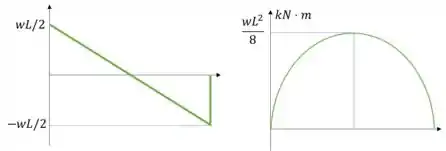
Passo 4
Momento de inércia da viga composta:
Passo 5
Vamos analisar a tensão normal gerada pelo momento:
Aplicando os valores:
A tensão calculada é maior que a tensão admissível. A viga não irá suportar.
Resposta
A viga não suporta o carregamento.
Exercícios de Livros Relacionados
As polias acopladas ao eixo estão carregadas como mostra a figura. Se os mancais em A e B exercem somente forças horizontais e verticais sobre o eixo, determine, com aproximação de 1m m , o diâmetro e
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60 MPa, determine, com aproximação de 1 mm, o eixo de menor diâmetro que suportará a carga. Use a teoria da
Os mancais em A e D exercem somente as componentes y e z da força sobre o eixo. Se τ a d m = 60M P a , determine, com aproximação de 1m m , o eixo de menor diâmetro que suportará a carga. Use a teoria
Resolva o Problema 11.38 usando a teoria de falha da energia de distorção máxima com σ m á x = 180M P a á .