Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 89

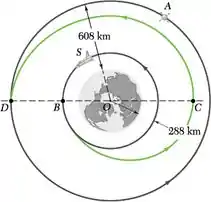
Um ônibus espacial S e um satélite A estão nas órbitas circulares mostradas na figura. Para poder recuperar o satélite, o ônibus espacial é primeiro colocado em uma trajetória elíptica BC, aumentando-se sua velocidade escalar em ∆ vB = 84 m/s quando ele passa por B. Quando o ônibus se aproxima de C, sua velocidade escalar é aumentada em ∆ vC = 78 m/s para inseri-lo em uma segunda órbita de transferência elíptica CD. Sabendo que a distância de O a C é de 6.860 km, determine o valor em que a velocidade escalar do ônibus deve ser aumentada quando ele se aproxima de D para que seja inserido na órbita circular do satélite.

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine o valor em que a velocidade escalar do ônibus deve ser aumentada quando ele se aproxima de D para que seja inserido na órbita circular do satélite.

R = 3960   mi = 20.9088 × 10 6   ft

r A = 3960 + 380   mi = 4340   mi = 22.9152 × 10 6   ft

r B = 3960 + 180   mi = 4140   mi = 21.8592 × 10 6   ft

Para uma órbita circular,

Σ F n = m a n :         F = m v 2 r

Eq. (12.28):

F = G M m r 2

Então

G M m r 2 = m v 2 r

ou

v 2 = G M r = g R 2 r                 usando a Eq. (12.29)

Então

( v A ) circ 2 = 32.2   ft/ s 2 × ( 20.9088 × 10 6   ft ) 2 22.9152 × 10 6   ft

ou

( v A ) circ = 24,785   ft/s

e

( v B ) circ 2 = 32.2   ft/ s 2 × ( 20.9088 × 10 6   ft ) 2 21.8592 × 10 6   ft

ou

( v B ) circ = 25,377   ft/s

Passo 2

Nós temos

( v B ) T R B C = ( v B ) circ + ∆ v B = 25,377 + 280   ft/s

= 25,657   ft/s

A conservação do momento angular requer que

B C :         r B m ( v B ) T R B C = r C m ( v C ) T R B C

C D :         r C m ( v C ) T R C D = r A m ( v D ) T R C D

Da Eq. (1)

( v C ) T R B C = r B r C ( v C ) T R B C = 4140   mi 4289   mi × 25,657   ft/s

= 24,766   ft/s

Agora

( v C ) T R C D = ( v C ) T R B C + ∆ v C = 24,766 + 260   ft/s

= 25,026   ft/s

Da Eq. (2)

( v D ) T R C D = r C r A ( v C ) T R C D = 4289   mi 4340   mi × 25,026   ft/s

= 24,732   ft/s

Finalmente,

( v A ) circ = ( v D ) T R C D + ∆ v D

Ou

∆ v D = 24,785 - 24,732   ft/s

Resposta

∆ v D = 53   ft/s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na prática, é frequentemente difícil determinar o decremento logarítmico de um sistema com o amortecimento subcrucial definido no Problema 19.129 pela medida de dois deslocamentos máximos sucessivos.
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo liberado de uma posição arbitrária com uma velocidade inicial arbitrária não pode passar mais de uma vez pela sua posição de equilí
Um disco de 30 kg é fixado, com uma excentricidade e = 0,15 mm,ao ponto médio de um eixo vertical AB que gira com uma velocidadeangular ω ƒ ƒ constante. Sabendo que a constante de mola k para o movime
Mostre que, no caso de amortecimento supercrucial (c c c ), um corpo nunca passa pela sua posição de equilíbrio O (a) se ele é liberado sem velocidade inicial de uma posição arbitrária, ou (b) se ele
No caso de amortecimento subcrucial, os deslocamentos x 1 , x 2 , x 3 mostrados na Fig. 19.11 podem ser considerados iguais aos deslocamentos máximos. Mostre que a razão de dois deslocamentos máximoss