Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 19.Problemas - Ex. 53

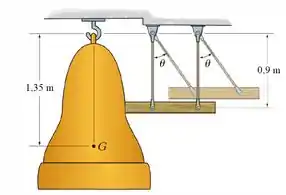
O sino de 150 kg está em repouso na posição vertical quando é atingido pela viga de madeira de 37,5 kg, suspensa por duas cordas de igual comprimento. Se a viga é solta do repouso em θ = 45 ° , determine a velocidade angular do sino e a velocidade da viga logo após o impacto. O coeficiente de restituição entre o sino e a viga é e = 0,6 . O centro de gravidade do sino está localizado no ponto G e seu raio de giração em relação a G é k G = 0,45   m .

Passo 1

Inicialmente, a viga se desloca de θ = 45 ° para θ = 0 ° para colidir com o sino. Em tal acontecimento, a energia mecânica é conservada. Tomando como referência a linha que passa pelo gancho do sino e suporte das cordas, temos:

T 1 + V 1 = T 2 + V 2

1 2 m v v v 1 2 + - W v y G 1 = 1 2 m v v v 2 2 + - W v y G 2

0 - 37,5 ( 9,81 ) 0,9 c o s 45 ° = 1 2 37,5 v v 2 2 - 37,5 ( 9,81 ) 0,9

v v 2 = 2,274   m / s

Passo 2

Uma vez que a soma dos impulsos angulares em torno do ponto O é igual a zero, então, o momento angular do sistema é conservado durante a colisão. Logo, deve-se a plicar a equação da conservação dos momentos angulares.

O momento de inercia do sino em torno do centro de massa ( G ) é

I G = m s k G 2 = 150 0,45 2 = 30,375   k g   . m 2

Assim,

( H O ) 2 = ( H O ) 3

[ m v v v ) 2 l v = [ m s v s ) 3 r s + I G ω s 3 + [ m v v v ) 3 l v

Logo ,

37,5 2,274   0,9 = 150 ω s 3 1,35 1,35 + 30,375 ω s 3 - 37,5 ( v v ) 3 0,9 eq.1

Passo 3

Por causa da colisão entre a viga e o sino deve-se aplicar a equação do coeficiente de restituição. Vale ressaltar que a velocidade do sino deve ser calculada no ponto de contato, então, ( v s ) p = 0,9 ω s 3 . Logo,

e = ( v s ) 3 p - ( v v ) 3 ( v v ) 2 - ( v s ) 2 p

0,6 = - 0,9 ω s 3 - ( v v ) 3 - 2,274   - 0

Resolvendo o sistema formado pelas equações (1) e (2), obtemos:

( v v ) 3 = 1,034   m / s

E

ω s 3 = 0,368   r a d / s

Resposta

A velocidade angular do sino é igual a 0,368   r a d / s e a velocidade da viga logo após o impacto é igual a 1,034   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O disco de hóquei no gelo com uma massa de 0,20k g tem uma velocidade de 12m / s antes de ser atingido pelo taco de hóquei. Após o impacto o disco se desloca na nova direção mostrada com uma velocidad
Uma espaçonave de 1000k g está viajando no espaço profundo com uma velocidade v e = 2000m / s quando um meteoro de 10k g se deslocando com uma velocidade v m de módulo 5000m / s na direção mostrada co
A quantidade de movimento linear total de um sistema de cinco partículas no instante de tempo t = 2,2s é dada por G 2,2 = 3,4i - 2,6j + 4,6kk g ∙ m / s . No instante de tempo t = 2,4s , a quantidade d
Os quatro sistemas deslizam sobre uma superfície horizontal lisa e possuem a mesma massa m . As configurações de massa nos dois pares são idênticas. O que pode ser dito sobre a aceleração do centro de
As duas esferas, cada uma com massa m , estão conectadas pela mola e barras articuladas de massa desprezível. As esferas estão livres para deslizar nas guias lisas subindo a inclinação θ . Determine a