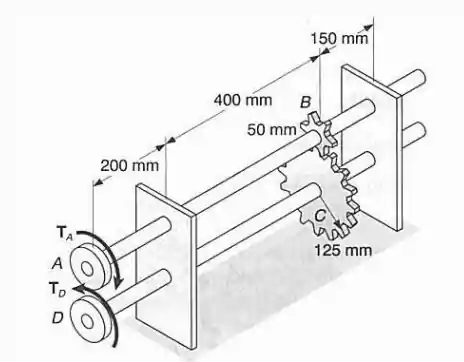
O sistema eixo-engranagem mostrado está sujeito a um torque de , enquanto que a polia é mantida fixa. Sabendo-se que , determinar o menor diâmetro permissível para o eixo .

Para começar o problema a gente vai ter que calcular a força que atuam na engrenagem , para isso vamos ter que utilizar aquela regrinha de que em engrenagens o torque é o mesmo e a força depende do tamanho do raio da engrenagem:

Como o torque vale vamos ter:

Com isso vamos fazer um desenho do nosso eixo com todas as forças que atuam sobre ele:

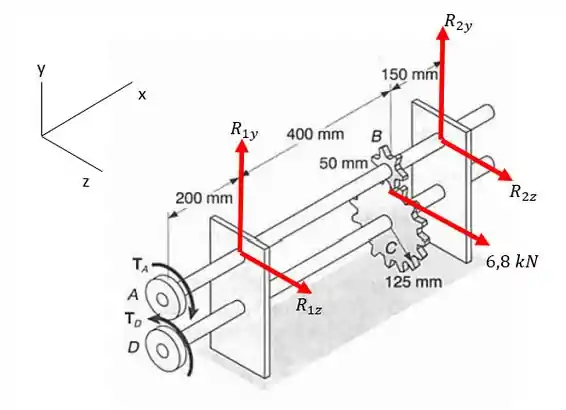
Agora vamos partir para as equações da estática.

utilizando as equações da estática vamos ter:

Repare que não existem forças em porque não há resistência nessa direção.

Resolvendo:

Para as forças em :

Beleza, não dá para ir muito além disso, agora vamos olhar os momentos. Aqui vamos calcular sempre o momento em relação ao nosso ponto ok? Onde estão as forças e .

Para o momento na direção em relação ao ponto :

Agora o momento em em relação ao ponto :

Pessoal, podemos parar por aqui! Já que achamos todas as forças que atuam no nosso eixo . Olha só!

Dessas equações a gente vai ter que:

Agora temos de calcular também os momentos fletores de cada seção. Mas aqui já fica uma dica, invés de calcular todos os pontos a gente pode pegar logo o ponto que é o ponto crítico do nosso problema. Então o momento fletor em vai ser igual a:

Agora vamos aplicar a relação entre torque e tensão cisalhante que é dada por:

Além disso a gente tem que lembrar do momento polar de inércia de eixos:

E

Assim,

Substituindo: