Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 51

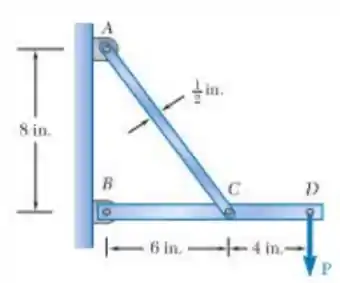
O vínculo AC é feito de aço com uma tensão normal última de 65 ksi e tem uma seção transversal retangular uniforme de ¼ x ½ in. Ele está conectado ao apoio em A e ao elemento BCD em C por pinos de 3/8 in de diâmetro, enquanto o elemento BCD é conectado a seu próprio apoio em B por um pino de 516 polegadas de diâmetro. Todos os pinos são feitos de aço com uma tensão de cisalhamento final de 25 ksi e estão em um cisalhamento único. Sabendo que um fator de segurança de 3,25 é desejado, determine a maior carga P que pode ser aplicada em D. Observe que o vínculo AC não é reforçado no entorno dos orifícios dos pinos.

Passo 1

E ai gurizada tudo belezinha??? Primeiramente vamos desenhar diagrama do corpo livre para termos uma ideia do comportamento :D

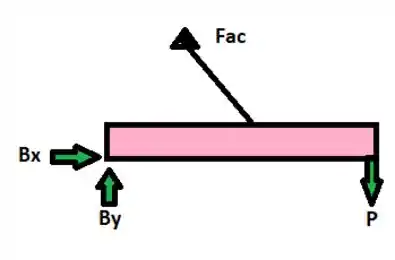
Primeiramente vamos realizar o somatório do momento em B , vem comigo :D

+ ↺ ∑ M b = F × d = 0

6 × 8 10   F a c - 10 P = 0

P = 0,48   F a c (1)

Agora partiu calcular o somatório das forças em x :D

+ ↑ ∑ F x = 0

B x - 6   F a c 10 = 0   (2)

Substituindo 1 em 2:

B x - 6   F a c 10 = 1,25   P

Realizando o somatório do momento em C , temos:

+ ↺ ∑ M c = F × d = 0

∑ M c =   - 6 B y - 4 P = 0

B y = 2 3 P

Sendo que B é calculado como:

B = B x 2 + B y 2    

B = 1,25 ² + 2 3 ² P    

P = 0,7   B

Passo 2

Tensão na seção de A e C

F a c = σ × A = σ F s × A = 65 3,25 × 1 4 × 1 2 - 3 8 = 0,625   k i p s

A menor força é a FAC então é a que usaremos:

P = 0,48 × 0,625 = 0,3   k i p s

Resposta

0,3   k i p s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força transversal P é aplicada, como mostrado, na extremidade A de um tronco de cone A B . Denotando por d 0 o diâmetro em A , mostre que a máxima tensão normal ocorre no ponto H , que está contido
Uma barra maciça de aço tem uma seção transversal trapezoidal e suporta uma carga uniformemente distribuída w como mostrado. Sabendo-se que σ a d m = + 75 M P a na tração e σ a d m = - 100 M P a na co
Sabendo-se que σ a d m = 160 M P a e τ a d m = 100 M P a , selecionar o perfil de abas largas que poderá ser usado para suportar o carregamento mostrado.
Resolva o problema 7.187, se cada uma das cargas de 20k N for aplicada separadamente na viga.
Para a viga com o carregamento mostrado, determinar: (a) a maior tensão normal devido à flexão; (b) a maior tensão de cisalhamento sobre uma seção transversal.