Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 1.Problemas - Ex. 47
Uma carga P é aplicada em um pino de aço que foi inserido em um elemento de madeira curto preso em um teto, como mostra a figura. O limite de resistência à tração da madeira utilizada é de 60 MPa e 7,5 MPa em cisalhamento, enquanto a resistência máxima do aço é de 145 MPa. Sabendo que b= 40 mm, c= 55 mm, d=12 mm, determinar a carga P se for desejado um coeficiente de segurança geral de 3,2
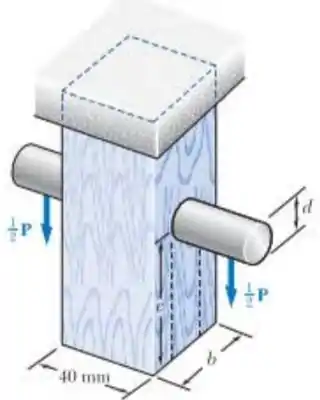
Passo 1
E ai gurizada tudo belezinha??? Considerando a base no cisalhamento duplo no pino, temos:
Com base na tensão na madeira
Baseado em cisalhamento duplo na corte
Usando o “P” de menor valor:
Tem-se:
Resposta
Exercícios de Livros Relacionados
Usando τ a d m = 50M P a , dimensionar um tronco de cone para o carregamento mostrado, determinando o diâmetro necessário: ( a ) em A ; ( b ) em B .
A viga A B C está fixada às vigas D B E e F C G . Sabendo-se que σ a d m = 165M P a e τ a d m = 100M P a , selecionar o perfil laminado de abas largas, que poderá ser usado: ( a ) para a viga A B C ;
Duas placas de cobertura, cada uma com 18m m de espessura e 220m m de largura, soldadas a uma viga de perfil laminado W 410 × 85 , como mostrado. Sabendo-se que σ a d m = 150M P a e τ a d m = 90M p a
Uma barra de 18m m de diâmetro deve ser encurvada devido às cargas aplicadas, como mostrado. Sabendo-se que P = 200N e Q = 0 , determinar a máxima tensão de cisalhamento e a máxima tensão normal, na e
Derivar a Eq. (733), a qual define a tensão vertical σ y , em uma viga retangular de largura unitária e altura 2 c , sujeita a uma carga distribuída w ( x ) .