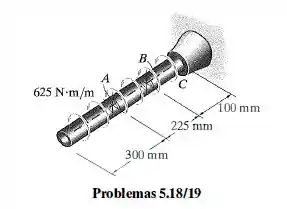
O tubo de cobre tem diâmetro externo de e diâmetro interno de . Se estiver firmemente preso à parede em e for submetido a um torque uniformemente distribuído ao longo de todo o seu comprimento, determine a tensão de cisalhamento máxima absoluta no tubo. Discuta a validade desse resultado.

Podemos pensar onde ocorre o maior torque nesse tubo. Concorda que é na extremidade , onde há reação? Isso porque ali temos o efeito de todo o torque aplicado em toda a extensão do tubo.

Só pensar, se você cortar sua barra em e olhar para extremidade onde tem o torque distribuído, o esforço interno resultante em vai ser a soma de todo esse torque ao longo da barra.

Assim, maior torque que podemos ter é considerando o tubo inteiro, então

Agora é só aplicar na fórmula. O cisalhamento vai ser máximo na borda do eixo .

Vamos pensar sobre esse resultado.

A fórmula da torção foi formulada segundo o princípio Saint-Venant, que só é válido em regiões distantes da aplicação de carregamentos concentrados.

Mas nós usamos o ponto onde há concentração de carregamento. Porque é nesse ponto onde há reação para o torque o produzido em todo eixo, já que temos ali um engaste.

Assim, ao usarmos o comprimento inteiro do tubo no cálculo da tensão máxima, estamos ignorando a concentração de tensão que com certeza ocorre próximo à parede, em .