Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 56
O soprador industrial aspira o ar através da arbetura axial com uma velocidade e o descarrega à pressão atmosférica e temperatura ambiente através do duto com de diâmetro com uma velocidade . O soprador movimenta de ar por minuto com o motor e o ventilador girando a . Se o motor exige de potência sem carga (ambos os dutos fechados), calcule a potência consumida enquanto o ar está sendo bombeado.
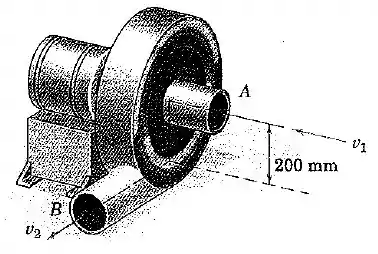
Passo 1
Se o motor exige de potência para funcionar com ambos os dutos fechados, a potência que precisamos calcular é a exigida para “acelerar” o ar que entra e sai do sistema.
Já que esse sistema envolve rotação, é uma boa ideia pensar em termos de momento. Na maior parte dos casos, a equação para o momento resultante é a seguinte:
Onde calculamos tudo em torno de algum ponto de referência, nesse caso, seria natural escolher o centro do ventilador de diâmetro .
Mas é importante lembrar de um detalhe: as velocidades dos fluxos não estão no mesmo plano! Por isso precisamos lembrar da definição mais geral do momento resultante:
Onde e são os vetores-posição dos das áreas de cada fluxo até o nosso referencial. Calma, é mais simples do que parece.
Passo 2
Vamos desenhar nosso sistema de outra forma:
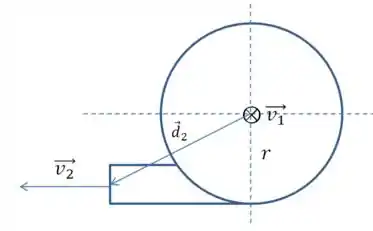
Vamos olhar de novo para a equação do momento:
O vetor está “entrando” no plano do papel, mas o vetor que liga o centro do nosso círculo até a área por onde o ar entra também está na mesma direção (veja o desenho do enunciado), isso significa que:
E agora podemos simplificar bastante nossa equação:
Tirando o módulo:
E como é o vetor que liga o centro do nosso círculo até o centro da área , o módulo desse produto vetorial é:
Onde é o ângulo entre os dois vetores. Beleza, agora já temos uma equação para o momento resultante:
Passo 3
Agora podemos calcular a taxa de escoamento de massa com os dados do enunciado.
E já que temos a cada minuto, ou a cada segundo, passando na abertura que tem diâmetro , a velocidade é:
E então o momento resultante é:
Passo 4
E agora é só calcular a potência associada a esse momento. Assim como o produto de força e velocidade é a potência no mundo das grandezas lineares, momento e velocidade angular são a potência no mundo das grandezas angulares:
E já que o motor consome por cona própria, a potência total vai ser:
Resolvido!
Resposta
A potência total consumida é .