Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 27
Determine a massa necessária do bloco de maneira que, ao ser solto do repouso, mova o bloco de 5 kg em uma distância de 0,75 m para cima ao longo do plano inclinado liso em s. Despreze a massa das polias e cordas.
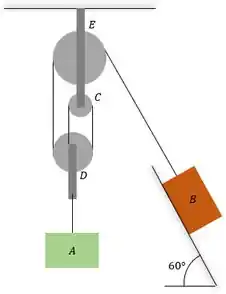
Passo 1
O enunciado nos dá as seguintes informações:
Massa do bloco : kg;
Distância percorrida: m;
Instante: s.
Devemos determinar a massa que o bloco deve ter para que mova o bloco por uma distância ao ser solto do repouso.
Como o bloco é solto do repouso em , sua velocidade inicial é de
O bloco também está em repouso nesse instante, logo
Passo 2
Sabemos que o bloco será puxado pela corda com uma aceleração .
Para encontrar essa aceleração, utilizaremos a equação da cinemática aplicada no eixo :
Portanto, temos que
Passo 3
Agora vamos encontrar a aceleração do com que o bloco se move.
Para isso, relacionaremos com utilizando uma análise de movimento dependente, que é discutida na seção 12.9 do livro.
Devemos escolher um ponto fixo no sistema e medir as posições de e . O ponto escolhido está representado no diagrama abaixo:
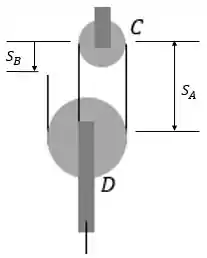
Portanto, temos que
Onde é o comprimento da corda e é constante.
Derivando esta equação duas vezes, podemos obter a aceleração de cada bloco, uma vez que
Logo, temos que
Substituindo o valor de , obtemos
Passo 4
Agora que já temos o valor da aceleração de cada bloco, vamos aplicar a Equação do Movimento para encontrar a tensão da corda.
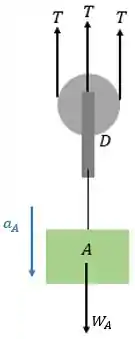
Primeiramente, vamos aplicar no bloco . O diagrama de corpo livre deve ser desenhado para melhor visualização do movimento:
Logo, temos que
Como ambos os blocos estáo ligados pelo mesmo cabo, a for;a é igual para ambos. Analisando o bloco e seu diagrama de corpo livre desenhado abaixo, temos que
