Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.8 - Ex. 106
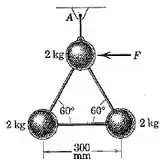
4/106) As três esferas idênticas de estão soldadas às hastes de conexão de massa desprezível e estão penduradas por um cordão a partir do ponto . As esferas estão inicialmente em repouso quando umaforça horizontal é aplicada à esfera superior . Calcule a aceleração inicial do centro de massa das esferas , a taxa na qual a velocidade angular está crescendo , e a aceleração inicial da esfera superior .
Passo 1
Então galera , a primeira coisa que devemos fazer é achar a distância entre a esfera mais elevada e centro de massa do sistema . Analisando o triângulo indicada na figura , obtemos que :
Logo ,
Para o sistema, temos que :
Portanto ,
Passo 2
Bom pessoal , nós sabemos que a resultante dos momentos em relação a deve ser igual a , a taxa de variação no tempo da quantidade de movimento angular do sistema, sendo assim :
Portanto ,
Além disso , nós sabemos que a aceleração linear é dada pela multiplicação entre a distância do ponto de aplicação da força até o centro de massa e a aceleração angular , logo :
Sendo assim ,