Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 53
Um carro esporte, tendo massa de 1700 kg, move-se horizontalmente ao longo de uma pista com uma inclinação de 20°, a qual é circular e tem um raio de curvatura de . Se o coeficiente de atrito estático entre os pneus e a estrada é de , determine a velocidade constante máxima na qual o carro pode se mover sem escorregar subindo a parte inclinada. Despreze a dimensão do carro.
Passo 1
A chave de problemas de cinética está no diagrama de corpo livre. Ao identificarmos todas as forças que o nosso problema está sujeito, conseguiremos visualizar o que há de ser feito mais facilmente.
Como o carro está em uma trajetória circular, ele estará sujeito a uma força centrípeta. Esta força tem que ser suficientemente grande para que o carro não deslize para cima na rampa. Relembrando do capítulo de cinemática, vimos que a aceleração centrípeta de um corpo é dada por:
Vamos a questão então!
Passo 2
Vamos começar por esboçar o diagrama de corpo livre. Sendo assim, temos:
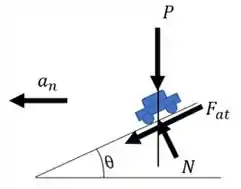
O nosso carro está sujeito a força peso para baixo, uma força normal, a qual é perpendicular ao plano, e uma força de atrito, o qual é paralelo ao plano e seu sentido é para baixo, pois ele é contrário ao movimento do carro (quer escorregar para cima).
Passo 3
Primeiramente, precisamos determinar o valor da força normal. Lembrando que a força de atrito é dada por:
Agora, vamos fazer um somatório de forças na direção do eixo , para cima. Nesta direção, temos:
Passo 4
Após determinarmos a força normal, vamos calcular o somatório de forças na direção do eixo , no qual temos uma aceleração centrípeta atuando no carro. Portanto, fazendo o somatório das forças nesta direção, obtemos: