Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas Fundamentais - Ex. 31
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta a viga medida a partir de .
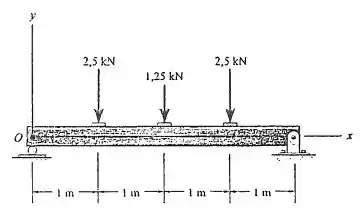
Passo 1
A questão pede para substituirmos o sistema de forças por uma única força resultante e especificar em que ponto essa força age. Como se trata se um sistema de forças paralelas, é possível fazer essa redução sem precisar adicionar um binário resultante.
O primeiro passo é calcular a força resultante:
Passo 2
O segundo passo é calcular o momento de binário resultante. Vale lembrar que o momento de uma força com relação ao ponto é dado por
Assim, o momento resultante com relação ao ponto será
Assim,
Portanto,
Passo 3
Agora precisamos achar o ponto que que a força resultante deve ser aplicada para compensar esse momento resultante:
Assim,
Assim, a força resultante deve ser aplica a uma distância do ponto .