Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 67
A força de está aplicada à extremidade do corpo . Se , determine o sistema força-binário equivalnte no eixo em .
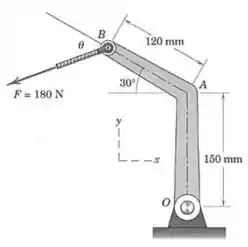
Passo 1
Bom, o primeiro elemento do nosso sistema força-binário é simplesmente uma força igual a , mas aplicada sobre o ponto .
A expressão para o vetor não muda quando ele é deslocado, então podemos procurar logo as componentes de :
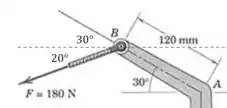
Passo 2
E o segundo elemento do nosso sistema é um binário que iguale o momento gerado pela força na sua posição inicial.
Para calcular esse momento total, vamos calcular o momento de cada uma das componentes da força .
Começando pela componente horizontal:
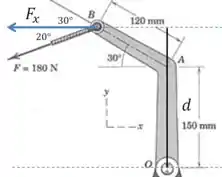
E agora vamos ver a componente vertical:
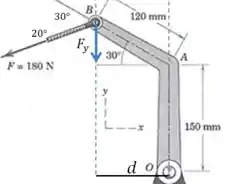
Passo 3
Então o momento total gerado pela força é:
E esse deve ser o módulo do nosso binário, voltado para o sentido anti-horário.
Resposta
Devemos ter e no sentido anti-horário.