Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas - Ex. 80
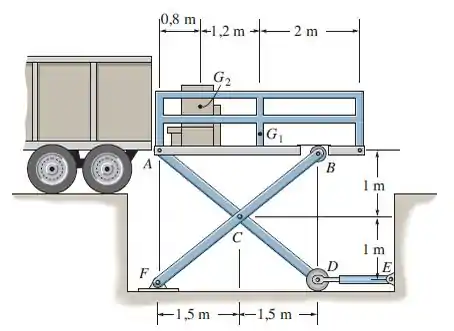
O dispositivo de elevação consiste em dois conjuntos de membros cruzados e dois cilindros hidráulicos, DE, localizados simetricamente em cada lado da plataforma. A plataforma possui massa uniforme de 60 kg, com centro de gravidade em . A carga de 85 kg, com centro de gravidade em , está localizada no centro entre cada lado da plataforma. Determine a força em cada um dos cilindros hidráulicos para que haja equilíbrio. Roletes estão localizados em e .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Devemos determinar a força em cada um dos cilindros hidráulicos . Como temos dois cilindros, ao desenharmos o nosso diagrama de corpo livre, vamos colocar 2 vezes a força! Cuidado para não esquecerem deste ponto.
Como vocês podem observar na questão, a nossa plataforma é composta por três partes. Temos a parte superior em que atuam os centros de massa, temos um braço e também temos um braço que contém os cilindros hidráulicos.
O que temos que fazer agora é esboçar o diagrama de corpo livre do braço e da parte superior, que contém os centros de massa.
Para o componente em que atuam os centros de massa, temos:
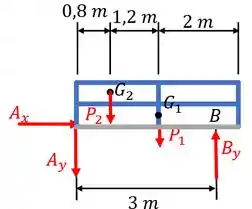
Começando pelo braço , temos:
Tenham muito cuidado ao colocarem as reações do pino em ambos os desenhos! Pela lei da ação e reação, eles devem ter sentidos contrários!
Agora que já temos todas as informações necessárias, vamos as contas!
Passo 2
Percebam que no diagrama de corpo livre do braço nós temos uma série de incógnitas!
Entretanto, como o braço está em equilíbrio, se fizermos o somatório de momentos em torno do ponto , o que eliminaria as reações da equação, reduziríamos as incógnitas para 3: , e (a que desejamos obter).
Portanto, se conseguirmos determinar e , conseguimos resolver o problema! E como faremos isto???
Simples, vamos aplicar as relações de equilíbrio para o diagrama de corpo livre que contém os centros de massa. Desta forma, temos:
E assim conseguimos descobrir as incógnitas e .
Passo 3
Para finalizarmos a questão, basta fazermos o que foi dito no Passo anterior. Isto é, fazermos o somatório de momentos em torno do ponto , para o diagrama do braço . Desta forma, temos:
E assim finalizamos a questão!