Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 142
Determine se o sistema de forças e binários mostrado na figura pode ser reduzido a uma força única equivalente . Se for o caso, determine e o ponto em que a linha de ação de intercepta o plano . Caso contrário, substitua o sistema dado por um torsor equivalente e determine sua resultante, seu passo e o ponto em que seu eixo intercepta o plano .
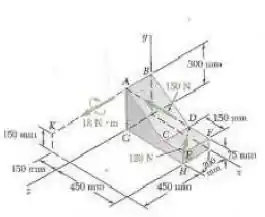
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro, vamos normalizar o vetor . Basta dividir cada componente do vetor pelo seu comprimento. O comprimento do vetor é dado pela raiz das somas dos componentes ao quadrado.
Agora vamos normalizar:
A força representada vetorialmente, será:
Passo 2
Vamos fazer o mesmo passo para os seguimentos e para representar a força e o momento na forma vetorial:
Agora vamos normalizar:
A força representada vetorialmente, será:
Para o segmento , temos:
Agora vamos normalizar:
O momento representado vetorialmente, será:
Passo 3
A resultante é dada então, por:
A intensidade da resultante será:
Passo 4
O torsor equivalente é calculado ao fazer o produto vetorial dos vetores que ultrapassam a distância das linha de ação das forças ao ponto . Somados aos torsores iniciados:
Substituindo os valores, temos:
Para que as forças originais possam ser reduzidas a uma força única, e devem ser perpendiculares. Ou seja, o produto vetorial entre e deve ser zero:
Fazendo os cálculos obtemos:
Portanto, o sistema não pode ser reduzido ao vetor .
Resposta
O sistema não pode ser reduzido ao vetor .