Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 41

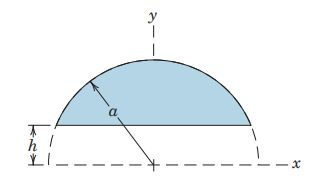
5.41. Determine the y-coordinate of the centroid of the plane area shown. Set h = 0 in your result and compare with the result y - = 4 a 3 π for a full semicircular area (see Sample Problem 5/3 and Table D/3). Also evaluate your result for the conditions h = a 4 and h = a 2 .

Passo 1

Beleza, nesse problema aqui procuramos a coordenada y do centroide.

y - = ∫ y c A d A  

Podemos começar identificando o elemento de área

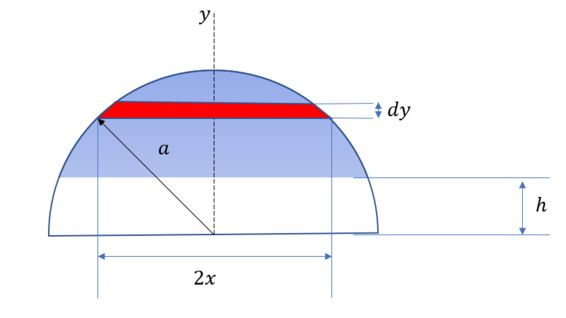
O elemento de área vai ser esse retangulozinho vermelho na imagem, e área dele é

d A = 2 x   d y

Passo 2

Vamos ver agora como a gente pode escrever esse x em termos de y . A figura que temos é um círculo, então sua função é do tipo

x 2 + y 2 = R 2

No caso do problema

x 2 + y 2 = a 2

Então

x = a 2 - y 2

Agora nós conseguimos calcular a área da figura

A = ∫ d A

Então

A = ∫ 2 x   d y

A = ∫ 2 a 2 - y 2   d y

A gente consegue ver na imagem os limites dessa integração

A = 2 ∫ h a a 2 - y 2 d y

Vamos fazer uma substituição para resolver essa integral

y = a sin ⁡ t d y = a cos ⁡ t   d t

A = 2 ∫ a 2 - a 2 sin 2 ⁡ t a cos ⁡ t d t

Podemos tirar o a de dentro da raiz

A = 2 ∫ 1 - sin 2 ⁡ t   a 2 cos ⁡ t d t

Agora vamos achar uma relação trigonométrica

1 - sin 2 ⁡ t = cos ⁡ t

E ficamos com

A = 2 ∫ a 2 cos 2 ⁡ t d t

Podemos simplificar um pouco mais

cos 2 ⁡ t = 1 2 1 + cos ⁡ 2 t

Então

A = a 2 ∫ 1 + cos ⁡ 2 t d t

Para resolver a gente só precisa fazer a substituição

2 t = u d t = d y 2

A = a 2 ∫ d t + ∫ 1 2 cos ⁡ u d u

Então ficamos com

A = a 2 t + 1 2 sin ⁡ u

Agora vamos desfazer as substituições

A = a 2 t + 1 2 sin ⁡ 2 t

A = a 2 t + sin ⁡ t cos ⁡ t

Bom, nós definimos

y = a sin ⁡ t

Então

t = arcsin ⁡ y a

Logo

A = a 2 arcsin ⁡ y a + sin ⁡ arcsin ⁡ y a cos ⁡ arcsin ⁡ y a

E isso fica

A = a 2 arcsin ⁡ y a + y a 1 - y 2 a 2

Agora vamos aplicar os limites

A = a 2 arcsin ⁡ y a + y a 1 - y 2 a 2 h a

A = a 2 arcsin ⁡ a a + a a 1 - a 2 a 2 - arcsin ⁡ h a + h a 1 - h 2 a 2

A = a 2 arcsin ⁡ 1 - arcsin ⁡ h a + h a 2 a 2 - h 2

E finalmente temos

A = a 2 π 2 - arcsin ⁡ h a - h a 2 - h 2

Passo 3

Agora que finalmente temos a área, basta determinar y - .

y - = ∫ y c A d A  

A y - = ∫ y ⋅ 2 a 2 - y 2   d y  

Vamos resolver mais essa integral

y - = 2 ∫ y a 2 - y 2   d y  

Agora temos uma multiplicação nessa integral, então vamos usar a estratégia da integração por partes

∫ u   d v = u ⋅ v - ∫ v   d u

Nesse caso temos

u = y d u = d y d v = a 2 - y 2 v = a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2

Pode parecer que é complicado fazer a integral de d v , mas a gente já fez uma integral muito parecida nesse mesmo problema, quando a gente estava calculando a área, é só pegar o resultado.

Então ficamos com

y - = 2 y ⋅ a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 - ∫ h a a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 d y

Vamos focar um minutinho na integral que está dentro dos colchetes

∫ h a a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 d y

Isso daqui fica

∫ h a a 2 2 arcsin ⁡ y a d y + ∫ h a y 2 a 2 - y 2   d y

Olha que interessante, o termo a direita é a repetição da integral que queremos resolver, lembra?

A y - = 2 ∫ y a 2 - y 2   d y  

Agora vamos escrever uma equação muito grande, mas não se assusto, logo ela vai se simplificar de novo

2 ∫ h a y a 2 - y 2   d y = 2 A y ⋅ a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 - ∫ h a a 2 2 arcsin ⁡ y a d y - ∫ h a y 2 a 2 - y 2 d y

Podemos cortar 2 , e passar os termos iguais para o mesmo lado

1 + 1 2 ∫ h a y a 2 - y 2   d y = y ⋅ a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 - ∫ h a a 2 2 arcsin ⁡ y a d y

Então

3 2 ∫ h a y a 2 - y 2   d y = y ⋅ a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 - ∫ h a a 2 2 arcsin ⁡ y a d y

Passo 4

Então só resta uma integral para a gente

∫ h a a 2 3 arcsin ⁡ y a d y

Aqui vamos de novo usar a regra do produto

u = arcsin ⁡ y a d u = 1 a 2 - y 2 d y d v = 1 v = y

E aí ficamos com

∫ h a a 2 3 arcsin ⁡ y a d y = a 2 2 y arcsin ⁡ y a - ∫ y 1 a 2 - y 2 d y

Agora vamos focar na integral a direita

∫ y 1 a 2 - y 2 d y

Aqui vamos fazer a substituição

t = a 2 - y 2 d t = - 2 y

Então

∫ y 1 a 2 - y 2 d y = ∫ y t d t - 2 y

A gente pode cortar o y

∫ y 1 a 2 - y 2 d y = - 1 2 ∫ d t t

Essa integral é mais fácil resolver

∫ y 1 a 2 - y 2 d y = -   t

Substituindo t

∫ y 1 a 2 - y 2 d y = -   t

∫ y 1 a 2 - y 2 d y = -   a 2 - y 2

Então ficamos com

∫ h a a 2 3 arcsin ⁡ y a d y = a 2 2 y arcsin ⁡ y a + a 2 - y 2

Passo 5

A gente já está quase acabando. A integral que a gente queria resolver inicialmente era

∫ h a y a 2 - y 2   d y = y ⋅ a 2 3 arcsin ⁡ y a + y a 2 a 2 - y 2 - ∫ h a a 2 3 arcsin ⁡ y a d y

E agora temos

3 2 ∫ h a y a 2 - y 2   d y = y ⋅ a 2 2 arcsin ⁡ y a + y a 2 a 2 - y 2 - a 2 2 y arcsin ⁡ y a + a 2 - y 2

A gente pode cortar o termo

y a 2 2 arcsin ⁡ y a

3 2 ∫ h a y a 2 - y 2   d y = y ⋅ a 2 2 y a 2 a 2 - y 2 - a 2 2 a 2 - y 2

E aí finalmente ficamos com

3 2 ∫ h a y a 2 - y 2   d y = y 2 2 a 2 - y 2 - a 2 2 a 2 - y 2

Agora vamos multiplicar tudo por 2 3

∫ h a y a 2 - y 2   d y = y 2 3 a 2 - y 2 - a 2 3 a 2 - y 2

Então

∫ h a y a 2 - y 2   d y = y 2 - a 2 3 a 2 - y 2

A gente pode simplificar ainda mais

∫ h a y a 2 - y 2   d y = - a 2 - y 2 3 a 2 - y 2

∫ h a y a 2 - y 2   d y = - a 2 - y 2 3 2 3

Aplicando os limites

∫ h a y a 2 - y 2   d y = - a 2 - a 2 3 2 3 + a 2 - h 2 3 2 3

∫ h a y a 2 - y 2   d y = a 2 - h 2 3 2 3

Passo 6

Agora vamos dar um passo para traz para organizar o pensamento. Queríamos calcular

A y - = ∫ h a y ⋅ 2 a 2 - y 2   d y

Então ficamos com

A y - = 2 ⋅ a 2 - h 2 3 2 3

Então

y - = 2 3 ⋅ a 2 - h 2 3 2 A

Agora vamos substituir a área

a 2 π 2 - arcsin ⁡ h a - h a 2 - h 2

y - = 2 3 ⋅ a 2 - h 2 3 2 a 2 π 2 - arcsin ⁡ h a - h a 2 - h 2

Passo 7

Finalmente temos uma expressão para y - , agora vamos analisar para os casos pedidos, primeiro para h = 0

y - = 2 3 ⋅ a 2 - ( 0 ) 2 3 2 a 2 π 2 - arcsin ⁡ 0 a - 0 a 2 - 0 2

Isso simplifica para

y - = 2 3 a 3 a 2 π 2 = 4 3 a π = 0,4244 a

E agora para o caso h = a 4

y - = 2 3 ⋅ a 2 - ( a 4 ) 2 3 2 a 2 π 2 - arcsin ⁡ a 4 a - a 4 a 2 - a 4 2

Então

y - = 2 3 a 3   1 - 1 16 2 a 2 π 2 - arcsin ⁡ 1 4 - 1 4 1 - 1 4

E finalmente

y - = 2 3 a   0,8789 1,3181 - 0,242 = 0,562 a  

E finalmente vamos analisar para o caso h = a 2

y - = 2 3 ⋅ a 2 - a 2 2 3 2 a 2 π 2 - arcsin ⁡ a 2 a - a 2 a 2 - a 2 2

Então

y - = 2 3 a 3   1 - 1 4 2 a 2 π 2 - arcsin ⁡ 1 2 - 1 2 1 - 1 2

E finalmente temos

y - = 2 3 a   0,5625 1 , 0472 - 0 , 35355 = 0 , 705 a  

Resposta

Para h = 0

y - = 0,4244 a  

Para h = a 4

y - = 0,562 a  

Para h = a 2

y - = 0,705 a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Localize o centroide y - da área sombreada.
Localize o centroide x - da área sombreada.
Localize o centroide x - da área.
Localize o centroide y ¯ da área sombreada. Resolva o problema calculando as integrais por meio da regra de Simpson.
Determine a distância y ¯ até o centro de gravidade do elemento homogêneo.