Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 102
Determine a área da superfície do meio-fio. Não inclua a área das extremidades no cálculo.
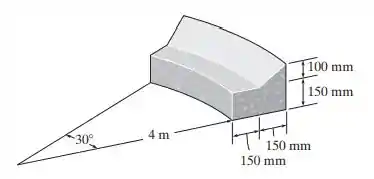
Passo 1
Fala aí, galerinha do Responde aí. Tudo bem? Bora pra mais uma questão de Estática.
Neste problema, temos que determinar a superfície de concreto do meio-fio. Para isso, vamos utilizar o teorema de Pappus Guldin, ele é dado por:
Onde é o ângulo de rotação que gera o corpo, neste caso, o meio-feio. Já é o perímetro da região que vai gerar o sólido e a distância do centroide da figura até o eixo de rotação.
Com isso, vamos determinar a área da região, temos:
Como podemos observar, esta região é composta por um retângulo e por um triângulo. Assim, o perímetro da região retangular vai ser:
Já para o perímetro da região triangular, temos que ulizar o teorema de Pitágoras para determinarmos a hipotenusa do triângulo, temos:
Logo, o perímetro vai ser:
Passo 2
Em seguida, temos a distância do braço de alavanca para o eixo. Sabemos que a distância até o eixo de rotação é de . Para a parte retangular, temos que a distância vai ser:
E para a parte triangular da região, temos:
Com isso, vamos utilizar o teorema de Pappus para cada uma das regiões. Para a região quadrada, a superfície vai ser:
E para a região triangular, temos:
Assim, a superfície total vai ser o somatório das duas superfícies das regiões. Fica assim:
É isso, galera, Bora resolver mais questões pra ficar craque.