Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 16

Qual superfície é representada por const. = r ∙ a , que é descrita se a é um vetor de magnitude constante e direção a partir da origem e r é o vetor de posição até o ponto P(x1, x2, x3) na superfície?

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.

r ∙ a = r a c o s   θ = c o n s t a n t e

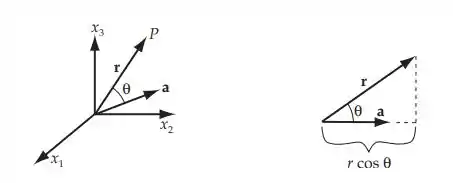
É dado que a é constante, então sabemos que:

r c o s   θ = c o n s t a n t e

Mas rcosθ é a magnitude da componente de r ao longo de a. O conjunto de vetores que satisfazem r ∙ a = c o n s t a n t e tem todos a mesma componente ao longo de a; entretanto, a componente perpendicular a a é arbitrária.

Logo:

A   s u p e r f í c i e   r e p r e s e n t a d a   p o r   r ∙ a = c o n s t a n t e   é   u m   p l a n o   p e r p e n d i c u l a r   a   a .

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Considere a, b, c como sendo três vetores constantes traçados a partir da origem até os pontos A, B e C. Qual é a distância da origem até o plano definido pelos pontos A, B, C? Qual é a área do triâng
Demonstre (veja também o Problema 1.11) que A B C = ∑ i j k ε i j k A i B j C k Obtenha a lei do cosseno da trigonometria plana interpretando o produto (A - B) . (A - B) e a expansão do produto.
Se r e r ˙ = v são ambas funções explícitas do tempo, demonstre que d d t r × ( v × r ) = r 2 a + r ∙ v v - v 2 + r ∙ a r
Considere A como sendo um vetor arbitrário e e como sendo um vetor unitário em alguma direção fixa. Demonstre que: A = e A ∙ e + e × A × e Qual é o significado geométrico de cada um dos dois termos da
Obtenha a lei do seno da trigonometria plana interpretando o produto A × B e a representação alternativa ( A - B ) × B .