Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 5
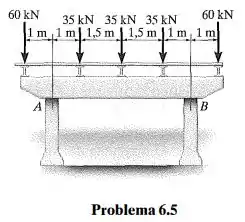
Um suporte de concreto armado é usado para apoiar as longarinas da plataforma de uma ponte. Represente graficamente os diagramas de força cortante e momento fletor para o suporte quando submetido à carga das longarinas mostradas na figura. Considere que as colunas em A e B exercem somente reações verticais no suporte.
Passo 1
Fala! Essa questão é para a gente fazer os diagramas de momento e cortante dessa viga. Tem um passo a passo para fazer isso. Só seguir, que dá bom!
Primeiro a gente precisa achar as reações no apoio nessa viga
Fazemos o diagrama de corpo livre:
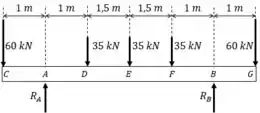
Como o carregamento e os apoios são perfeitamente simétricos:
Aplicando o somatário de forças:
Passo 2
Quando temos muitas cargas pontuais espaçadas, é mais fácil desenhar o diagrama de esforços pelo método gráfico.
O valor do cortante em cada ponto crítico (onde temos força concentrada) é a soma vetorial(considerando se está para baixo ou para cima) das forças anteriores.
Colocamos os pontos no gráfico:
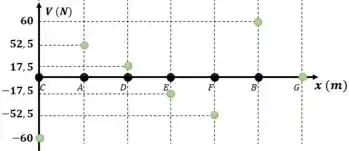
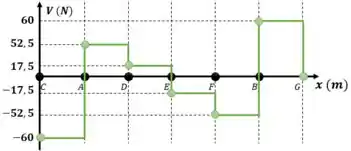
Como as cargas são pontuais, elas são representadas no gráfico de esforço cortante como retas paralelas ao eixo X, que se estendem até o ponto seguinte:
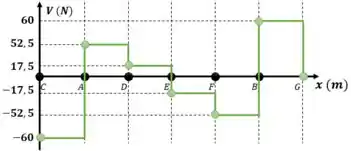
Passo 3
O gráfico de momento fletor é a integral do gráfico de esfoço cortante. Então, podemos calcular a intensidade do momento fletor calculando a área abaixo do gráfico de esforço cortante. Então, vamos calcular a área abaixo de todas as seções do gráfico de esforço cortante e depois contruir o gráfico de momento fletor.
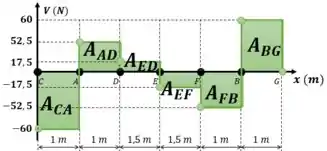
Com o valor das áreas, podemos calcular o momento em cada ponto. Eles vão ser dados pela soma algébrica de cada área antes do ponto em questão.
Distribuímos os pontos em no plano cartesiano
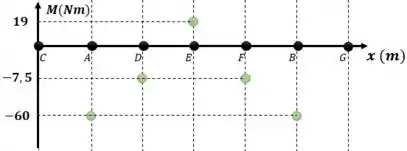
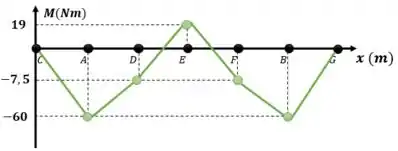
Como as linhas no gráfico de esforço cortante representam constantes, e a integração de constantes são retas inclinadas, vamos ligar os pontos do gráfico com retas:
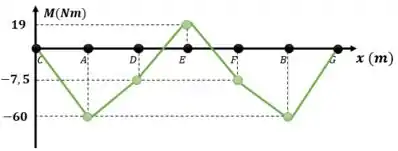
Resposta
