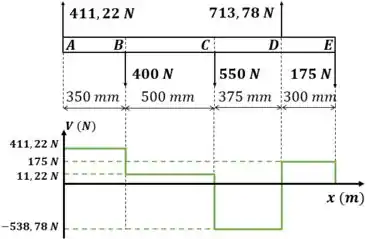
Represente graficamente os diagramas de força cortante momento fletor para o eixo. Os mancais em A e D exercem somente reações verticais sobre o eixo. A carga aplicada às polias em B, C e E
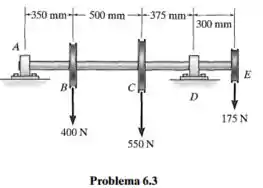
Passo 1
Começamos com um diagrama de corpo livre
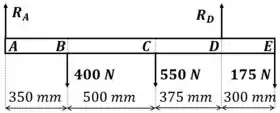
E calculamos as reações em A e D:

Passo 2
Agora vamos desenhar os gráficos de esforços internos pelo método gráfico. De acordo com a Tabela 6.1
Primeiro desenhamos o diagrama de corpo livre, e logo abaixo desenhamos um eixo coordenado . Então seccionamos este eixo com linhas pontilhadas de acordo com a distribuição de carregamento sobre a viga.

Agora observamos a primeira seção . Observe que no ponto A existe um carregamento local e positivo. Isso é representado por uma linha reta no gráfico de momento:
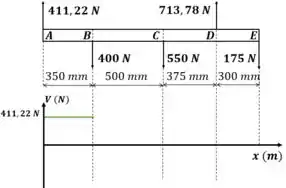
Quando chegamos no ponto B, temos uma carga local e negativa. Isso diminui a força interna na viga. No gráfico isso é representada por uma queda vertical
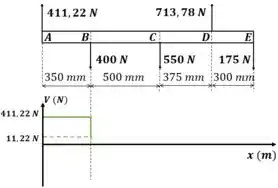
E, similarmente, a carga interna se mantém constante até que uma nova carga externa apareça.
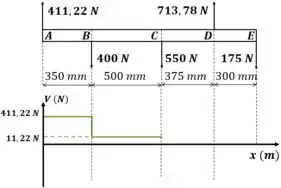
Esse processo é repetido até completar o gráfico:
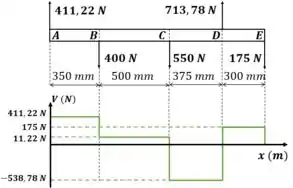
Passo 3
Para desenhar o gráfico do momento fletor, primeiro geramos os eixos coordenados abaixo do gráfico de esforço cortante:
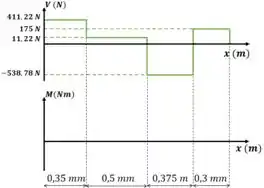
O gráfico de momento fletor é a integral do gráfico de esforço cortante. Então, podemos calcular a intensidade do momento fletor calculando a área abaixo do gráfico de esforço cortante. Então, vamos calcular a área abaixo de todas as seções do gráfico de esforço cortante e depois construir o gráfico de momento fletor.
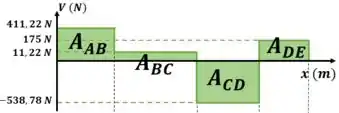
Com os valores das áreas podemos calcular o gráfico de momento fletor
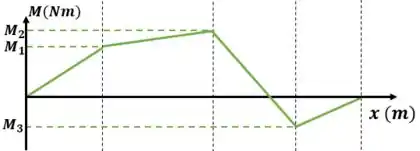
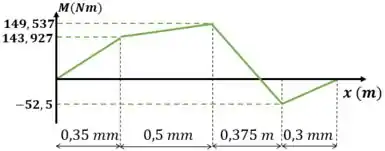
Resposta