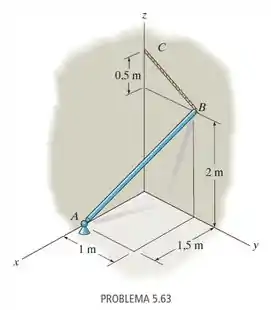
5.63. A haste uniforme lisa AB é apoiada por uma junta esférica em A, a parede em B e o cabo BC. Determine as componentes da reação em A, a tensão no cabo e a reação normal em B, se a barra possui massa de 20 kg.
Passo 1
Falaaa... belezinha???
Nessa questão a gente vai usar:
- Somatório das forças é igual a zero:
- Somatório dos momentos em A é igual a zero:
E vamos mandar um diagrama de corpo livre maroto:
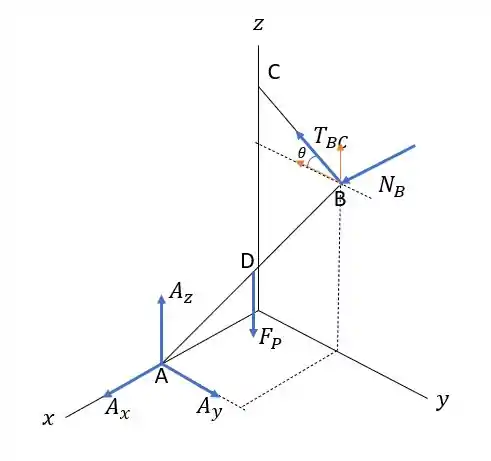
Passo 2
Vamos colocar tudo nas suas coordenadas pra organizar e a gente não errar, ok?
Repara que a tração na corda a gente pode decompor em y e z:
Como é e o outro , então a hipotenusa a gente acha por Pitágoras mesmo:
Então já temos o seno e cosseno do ângulo:
A força peso da barra calculamos usando :
E já vamos pegar os vetores pra calcular o momento:
Passo 3
E vamos aos cálculos...
Para a soma das forças:
Daí podemos montar o sisteminha:
Para o momento em A:
E montamos outro sisteminha:
Resolvendo a primeira equação:
Agora pegando a terceira equação:
Agora é só ser feliz pegando as equações do primeiro sistema:
Showww... Deu um pouco de trabalho, né?? Mas se fizer arrumadinho dá pra ir aos poucos.
Desanima nãoo... Bora pra próxima.