Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 87

Um suporte isolador de vibração consiste em uma barra A de raio R 1 = 10   m m e um tubo B de raio interno R 2 = 25   m m , colado a um tubo de borracha de 80 mm de comprimento com um modulo de elasticidade transversal G = 12   M P a . Determine a maior força P admissível que pode ser aplicada à barra A, sabendo que seu deslocamento não deve exceder 2,50 mm.

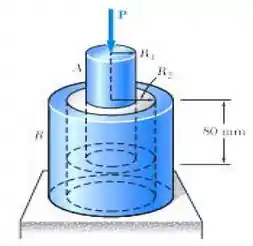
Passo 1

Fala aí gurizada tudo belezinha? O enunciado pede que a gente determine a maior força P admissível, então vamos esboçar o diagrama de corpo livre, vem comigo :D

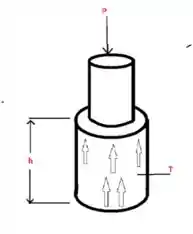
Seja r uma coordenada radial. Sobre o cilindro oco de borracha, consideramos que:

R 1 ≤ r ≤ R 2 .

A tensão de cisalhamento τ atuando em uma superfície cilíndrica de raio r é

τ = P A = P 2 π r h

Então

γ = τ G = P 2 π G h r

Deformação por cisalhamento ao longo do comprimento radial d r como representado na imagem a seguir:

d δ d r = γ d δ = γ d r = P 2 π G h   x   d r

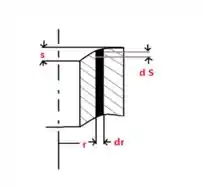
Passo 2

A deformação total é dada por:

δ = ∫ R 2 R 1   d δ = P 2 π G h ∫ R 2 R 1   d r r = P 2 π G h     n o     r R 2 R 1 P 2 π G h (   n o   R 2 - n o   R 1 ) = P 2 π G h   n o   R 2 R 1         o u       P = 2 π G h δ n o (   R 2 / R 1 )

Trazendo os seguintes dados temos: R 1 = 100   m m = 0,010   m ,   R 2 = 25   m m = 0,025   m ,   h = 80   m m = 0,080 m ,   G = 12   x   10 6 P a           δ = 2,50   x   10 - 3 m

Podemos determinar P :D P = 2 π   x   12   x   10 6   x   0,080   x   ( 2,50   x   10 - 3 ) n o   ( 0,025 / 0,010 ) = 16,46   x   10 3 N

Resposta

16,46   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As deformações principais em um ponto sobre a superfície de alumínio de um tanque são ϵ 1 = 630 ( 10 - 6 ) e ϵ 2 = 350 ( 10 - 6 ) . Se for um caso de estado plano de tensão, determine as tensões princ
Uma carga periférica uniforme de 100kN/m e 70kN/m é aplicada a um corpo de prova de poliestireno. Se a forma original do corpo de prova for quadrada, de dimensões a = 50mm , b = 50mm e espessura t = 6
As tensões principais em um ponto são mostradas na figura. Se o material for grafite, para o qual E g = 5,6GPa e ν = 0,23 , determine as deformações principais.
Uma haste tem raio de 10mm . Se for submetida a uma carga axial de 15N tal que a deformação axial na haste seja ϵ x = 2,75 ⋅ 10 - 6 , determine o módulo de elasticidade E e a mudança em seu diâmetro.
A haste é feita de alumínio 2014 -T 6 . Se for submetida à carga de tração de 700N e tiver diâmetro de 20mm , determine a deformação por cisalhamento máxima absoluta na haste em um ponto sobre sua sup