Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 84

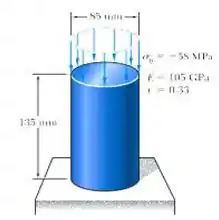
Para o carregamento axial mostrado, determine a variação em altura e a variação em volume do cilindro de latão mostrado na figura, (b) resolva a parte a considerando que o carregamento seja hidrostático com σ x = σ v = σ τ = - 70   M P a .

Passo 1

Fala ai gurizada tudo beleza? O exercício pede para que a gente determine a variação em altura e a variação em volume do cilindro de latã, sabendo que a altura do cilindro é de h 0 = 135 m m = 0,135   m , vamos então determinar a a área e o volume deste elemento:

A 0 = π 4 d 0 2 = π 4   x   85 2 = 5,6745   x   10 3 m m 2 = 5,6745   x   10 - 3 m 2 V 0 = A 0 h 0 = 766,06   x   10 3 m m 3 = 766,06   x   10 - 6 m 3

Sabendo que a tensão é σ x = 0 ,   σ y = - 58   x   10 6 P a ,   σ z = 0 , vamos determinar a deformação em y deste material:

ε y = 1 E - v σ x + σ y - v σ z = σ y E = - 58   x   10 6 105   x   10 9 = - 552,38   x   10 - 6

Temos que a variação de altura é de:

∆ h = h 0 ε y = 135 m m x   - 552,38   x   10 - 6 = - 0,0746   m m

Onde: e = 1 - 2 v E   x   σ x + σ y + σ z = 1 - 2 v σ y E = 0,34 x   - 58   x   10 6 105   x   10 9 = - 187,81   x   10 - 6

Temos que a variação de volume é de:

∆ V = V 0 e = 766,06   x   10 3 m m 3 x   ( - 187,81   x   10 - 6 ) = - 143,9 m m 3

Passo 2

Considerando as tensões

σ x = σ y = σ z = - 70   x   10 6 P a           σ x + σ y + σ z = - 210   x   10 6 P a

Vamos determinar a deformação em y deste material:

ε y = 1 E   x   – v σ x + σ y - v σ z =   1 - 2 v E σ y = 0,34 x - 70   x   10 6 105   x     10 9 = - 226,67   x     10 - 6

Temos que a variação de altura é de:

∆ h = h 0 ε y = 135 m m x   - 226,67     x   10 - 6 = - 0,0306 m m

Onde:

e = 1 - 2 v E   x   σ x + σ y - σ z = 0,34   x   - 210   x   10 6 105     x   10 9 = 680   x   10 - 6

Temos que a variação de volume é de:

∆ V = V 0 e = 766,06   x   10 - 6   x   ( - 680   x   10 - 6 ) = - 521 m m ³  

Resposta

(a) ∆ h =   - 0,0746   m m   e   ∆ V = - 143,9 m m 3

(b) ∆ h = - 0,0306 m m   e   ∆ V = - 521 m m ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A variação no diâmetro de um grande parafuso de aço é cuidadosamente medida enquanto a porca é apertada. Sabendo que E = 29x10 6p s i e v = 0,30 , determine a força interna no parafuso, quando se obse
Em um ensaio de tração padrão, uma barra de aço de 22m m de diâmetro está submetida a uma força de tração de 75k N . Sabendo que v = 0,30eE = 200G P a , determine (a) o alongamento da barra em um comp
Um tubo de alumínio de comprimento igual a2 m , diâmetro externo de 240 - m m e espessura de parede de 10 - m m é usado como uma coluna curta e suporta uma força axial centrada de 640 - k N . Sabendo
Uma força de tração de 2,75k N é aplicada a um corpo de prova feito de placa de aço plana de 1,6m m ( E = 200G P a ,v = 0,30 ) . Determine a variação resultante (a) no comprimento de referência de 50m
Para um elemento sob carga axial, expresse a deformação normal ϵ ' em uma direção que forma um ângulo de 45° com o eixo de carga em função da deformação axial ϵ fazendo (a) a comparação da hipotenusa