Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 59

Determine (a) a força de compressão nas barras mostradas depois que a temperatura atingiu 82°C e (b) a variação correspondente no comprimento da barra de bronze.

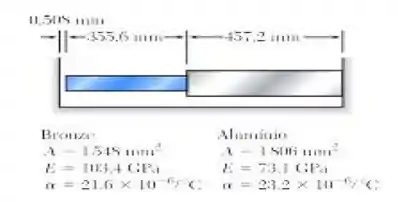
Passo 1

Fala aí galerinha tudo belezinha? Para determinarmos a força compressiva na barra, vamos primeiramente determinar encurtamento, vejam o esboço abaixo :D

Expansão térmica se livre de restrições:

δ T = L b   ∝ b ∆ T +   L a α a ∆ T = 3,556   x   21,6   x   10 - 6     x     82 +   4,572   x   23,2   x   10 - 6     x   82 = 15   x   10 - 3   m

Expansão restrita: δ = 0,508   m m

Encurtamento devido à força compressiva é determinada como:

δ P = 7 15   x   10 - 3   m - 5 , 08 x   10 - 4   = 714,5   x   10 - 3   m .

Passo 2

Seja o alongamento após a forca compressiva P temos:

δ P = P L b E b A b + P L a E a A a = L b E b A b + L a E a A a P 3,556 103,4   x   10 9     x   15,48 + 4,572 73,1   x   10 9     x     18,06 P = 714,5   x   10 - 3    

Igualando para encontrarmos P temos:

                                                          ( 2,22 x   10 - 12 + 3,463 x   10 - 12 ) P = 714,5   x   10 - 3 a) P = 125,722   x   10 9     P a

B )   δ b =   L b α b   x   ∆ T - P L b E b A b = 0,252   m m  

Resposta

  1. P = 125,722   x   10 9     P a
  2. δ b = 0,252   m m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As barras A B e B C são feitas de um aço para o qual a tensão de escoamento é σ E = 300M P a e o módulo de elasticidade é E = 200G p a . Determine a máxima energia de deformação que pode ser adquirida
Um tubo de alumínio com comprimento de 762m m e seção transversal de área de 1194m m 2 é soldado a um suporte fixo A e a uma tampa rígida B . A barra de aço E F , de 19,1m m de diâmetro, é soldada à t
A montagem A B C é feita com um aço para o qual E = 200G P a e σ E = 320M P a . Sabendo que a montagem deve absorver uma energia de deformação de 5J na medida em que se aplica à carga P , determine o
Mostre, por integração, que a energia de deformação da barra cônica A b ´r: U = 1 4 P 2 L E A m i n Em que A m i n é a área transversal em B .
Na treliça mostrada, todos os elementos são feitos do mesmo material e têm a área da seção trasnversal indicada. Determine a energia de deformação da treliça quando lhe é aplicada a força P .