Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 13

A tábua de cerca está entrelaçada entre os três mourões lisos fixos. Se os mourões estiverem instalados ao longo da mesma linha reta, determine a tensão de flexão máxima na tábua. A largura e a espessura da tábua são 150   m m e 12   m m , respectivamente. E   =   12   G P a . Considere que o deslocamento de cada extremidade da tábua em relação a seu centro seja 75   m m .

Passo 1

Fala, querido! Vamos entender o que está acontecendo. Temos uma barra. Podemos interpretar ela como biapoiada, mas tendo algo ai no meio que obriga a deflexão na metade ser 75   m m (o diâmetro desse mourão).

v m e i o = 75   m m

E aí, a gente pode pensar: se não tivesse esse cara no meio, que força P   eu aplicaria para causar esse mesmo valor de deflexão? Para chegar nessa força, a gente precisa analisar as deflexões de uma viga biapoiada com a carga P   no meio.

Por simetria, a gente sabe que as reações vaem P / 2

Sabendo essa força P , nós achamos o momento máximo nessa barra (que vai ocorrer no meio) e assim a tensão máxima de flexão como o enunciado pede.

Passo 2

Vamos então achar as equações das linhas elásticas em função de P .

Para 0 ≤ x 1 ≤ 1,2   m :

∑ M = 0 M x 1 - P 2 x 1   = 0 M x 1 = P 2 x 1

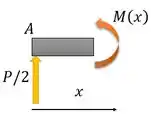
Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = P 2 x 1

E I d v 1 d x 1 = P 4 x 1 2 +   C 1

E I v 1 = P 12 x 1 3 + C 1 x 1 + C 2

Para 0 ≤ x 2 ≤ 1,2   m :

∑ M = 0 - M x 2 + P 2 x 2 = 0 M x 2 = P 2 x 2

Logo:

E I d 2 v 2 d x 2 2 = P 2 x 2

E I d v 2 d x 2 = P L 4 x 2 2 + C 3

E I v 2 = P L 12 x 2 3 + C 3 x 2 + C 4

Passo 3

As condições de contorno serão:

x 1 = 0 → v 1 = 0

x 2 = 0 → v 2 = 0

Já que nos apoios a deflexão deve ser nula.

Já as condições de continuidade serão:

x 1 = x 2 = 1,2 →     d v 1 d x 1 = - d v 2 d x 2

Porque as equações devem ter valores iguais em pontos iguais.

Logo, substituindo:

E I v 1 = P 12 x 1 3 + C 1 x 1 + C 2 → 0 = 0 + 0 + C 2 → C 2 = 0

E I v 2 = P L 12 x 2 3 + C 3 x 2 + C 4 → 0 = 0 + 0 + C 4 → C 4 = 0

P 12 x 1 3 + C 1 x 1 = P L 12 x 2 3 + C 3 x 2 → P 12 x 1 3 + C 1 1,2 3 = P L 12 x 2 3 + C 3 1,2 3

P L 4 x 2 2 + C 3 = P 4 x 1 2 +   C 1 → P L 4 1,2 2 + C 3 = P 4 1,2 2 +   C 1 → C 1 = C 3

Resolvendo o sistema:

C 1 = - 0,36 P ; C 3 = - 0,36 ;

Passo 4

Agora, vamos usar v 1 :

v 1 = P 12 x 1 3 - 4,32 x 1

Para x 1 = 1,2 m , ou seja, no meio da barra, precisamos ter:

v 1 = 75   m m

Fazemos então:

75 10 - 3 = P 12 1,2 3 - 4,32 1,2

Isolando P :

P = 67,5   N

Passo 5

O momento no meio da viga (momento máximo para esse caso), é:

M m á x = P L 2

M m á x = 67,5 2 1,2

M m á x = 40,5   N . m

Sendo assim:

c = 12 2 m m

σ m á x = M m á x c I = 40,5 × 0,006 0,15 × 0,012 3 12 = 11,25   M P a

Resposta

σ m á x = 11,25   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a inclinação em A . E I é constante.
Determine as equações da linha elástica utilizando as coordenadas x 1 e x 3 e especifique a inclinação e a deflexão no ponto B . E I é constante.
O eixo é suportado em A por um mancai de a oio que exerce somente reações verticais sobre o eixo em B por um mancal de encosto que exerce reações horizontais verticais sobre o eixo. Trace o diagrama d
Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a inclinação e a deflexão em B . E I é constante.
Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a deflexão e a inclinação em C . E I é constante.