Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 17

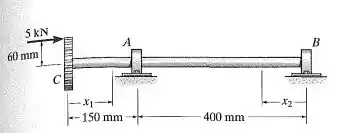
O eixo é suportado em A por um mancai de a oio que exerce somente reações verticais sobre o eixo em B por um mancal de encosto que exerce reações horizontais verticais sobre o eixo. Trace o diagrama de momento fletor para o eixo e a seguir, por esse diagrama, trace a curva e deflexão ou linha elástica para a linha central do eixo. Determine as equações da linha elástica usando as coordenadas x 1 e x 2 . E I é constante.

Passo 1

Para 0 ≤ x 1 ≤ 0,15   m :

∑ M = 0 M x 1 - 300   = 0 M x 1 = 300

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = 300

E I d v 1 d x 1 = 300 x 1 +   C 1

E I v 1 = 150 x 1 2 + C 1 x 1 + C 2

Para 0 ≤ x 2 ≤ 0,4   m :

∑ M = 0 M x 2 - 750 x 2 = 0 M x 2 = 750 x 2

Logo:

E I d 2 v 2 d x 2 2 = 750 x 2

E I d v 2 d x 2 = 375 x 2 2 + C 3

E I v 2 = 125 x 2 3 + C 3 x 2 + C 4

Passo 2

As condições de contorno serão:

x 1 = 0 , 15   m → v 1 = 0

x 2 = 0,4   m → d v 1 d x 1 = - d v 2 d x 2

Já as condições de continuidade serão:

x 1 = 0,15   m   e   x 2 = 0,4   m ;   d v 1 d x 1 = - d v 2 d x 2

Logo, substituindo:

C 1 = - 85 ; C 2 = 9,375 ; C 3 = - 20 ; C 4 = 0

Passo 3

Por fim, vamos substutiuir as constantes nas equações da linha elástica, obtem-se:

v 1 = 1 E I 150 x 1 2 - 85 x 1 + 9,375 N . m 3 E para x 2 :

v 2 = 1 E I 1 25 x 3 3 - 20 x 2 N . m 3

Resposta

v 1 = 1 E I 150 x 1 2 - 85 x 1 + 9,375 N . m 3

v 2 = 1 E I 125 x 3 3 - 20 x 2 N . m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga simplesmente apoiada A B é carregada com uma carga distribuída que varia linearmente como mostrado. Determinar:A equação da linha elástica;A deflexão no ponto médio do vão;A declividade na extr
A viga simplesmente apoiada A B é carregada com uma carga distribuída que varia linearmente como mostrado. Determinar:A equação da linha elástica;A deflexão no ponto médio do vão;A declividade na extr
Para a viga com o carregamento mostrado, determinar a deflexão no: a) ponto A b) ponto C.
Para a viga com o carregamento mostrado, determinar a reação no apoio móvel e a deflexão no ponto c.
Para a viga com o carregamento mostrado, determinar a deflexão no ponto A.