Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 18

Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a deflexão e a inclinação em C . E I é constante.

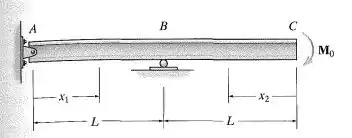
Passo 1

Em um primeiro passo, vamos usar a equação de momento em A e as equações de equilíbrio:

∑ M A = 0 F B - M 0 L   = 0 F B = M 0 L

∑ F y = 0

- F A + F B = 0 F A = F B = M 0 L

Para 0 ≤ x 1 ≤ L :

∑ M = 0 M x 1 + M 0 L x 1 = 0 M x 1 = - M 0 L x 1

Sabendo que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = M 0 L x 1 2

E I d v 1 d x 1 = - M 0 2 L x 1 2 +   C 1

E I v 1 = M 0 6 L x 1 3 + C 1 x 1 + C 2

Para 0 ≤ x 2 ≤ L :

∑ M = 0 - M x 2 - M 0 = 0 M x 2 = - M 0

Logo:

E I d 2 v 2 d x 2 2 = - M 0

E I d v 2 d x 2 = - M 0 x 2 + C 3

E I v 2 = - M 0 2 x 2 + C 3 x 2 + C 4

Passo 2

As condições de contorno serão:

x 1 = 0 = L → v 1 = 0

Já as condições de continuidade serão:

x 1 = x 2 = L → v 1 = v 2 = 0 e     d v 1 d x 1 = - d v 2 d x 2

Logo, substituindo:

C 1 = M 0 L 6 ; C 2 = 0 ; C 3 = 4 3 M 0 L   ; C 4 = - 5 6 M 0 L 2

Passo 3

Para as equações da linha elástica, temos:

v 1 = M 0 6 E I L - x 1 + L 2 x 1

E para v 2 :

v 2 = M 0 6 E I L ( - 3 L x 2 3 + 8 L 2 x 2 - 5 L 3 )

E assim, temos que a deflexão em C, ocorre em x 2 = 0 :

v c = - 5 M 0 P L 2 6 E I

Já a inclinação em C , ocorre em x 2 =0:

θ C = 4 M 0 L 2 3 E I

Resposta

v 1 = M 0 6 E I L - x 1 + L 2 x 1

v 2 = M 0 6 E I L ( - 3 L x 2 3 + 8 L 2 x 2 - 5 L 3 )

v c = - 5 M 0 P L 2 6 E I

θ C = 4 M 0 L 2 3 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar a) a equação da linha elástica b) a deflexão no ponto médio C.
Para a viga constituída de um perfil laminado de aço W610 x 101 e o carregamento mostrado, determinar: a) a declividade na extremidade A b) deflexão no ponto médio C. Usar E= 200 GPa
A barra rígida DEF é soldada ao ponto D da viga constituída de um perfil laminado de aço AB. Para o carregamento mostrado, determinar a) a declividade em A b) a deflexão do ponto médio C da viga. Usar
Para a viga com o carregamento mostrado, determinar a) a equação da linha elástica b) a deflexão no ponto médio C.
Determinar a reação de apoio em A e desenhar os diagramas de momento fletor.