Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 6

Para uma alavanca de câmbio mostrada na figura determine a intensidade e direção da menor força P que gera um momento no sentido horário de 24   N ⋅ m sobre B.

Passo 1

Do diagrama do corpo livre:

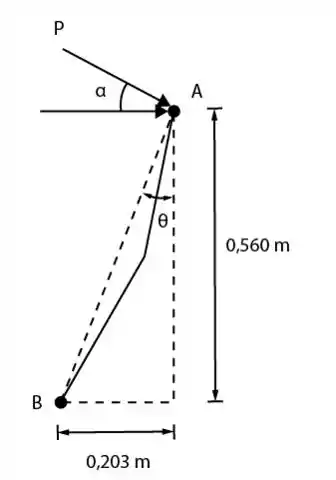
Passo 2

Vamos começar calculando a distância A B :

A B = 203 2 + 560 2 = 595,66   m m = 0,596   m C a l c u l a n d o   o   â n g u l o   f e i t o   e n t r e   A B e a horizontal

θ = arctan ⁡ (   0,560 0,203 ) = 70,07 º

Passo 3

Para que P seja mínimo, a carga aplicada no fim alavanca precisa ser perpendicular à linha A B . Calculando o momento sobre o ponto B:

M B = P × A B

Substituindo o momento M B = 24   N ⋅ m e A B = 0,596

M B = P ⋅ A B 24 = P ⋅ 0,596 P = 40,27   N

Passo 4

Da geometria:

α + θ = 90 º

Onde α é a direção da menor força.

Substituido θ = 70 º :

70 + α = 90 º α = 20 º

Resposta

P = 40,27   N α = 20 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento resultante produzido pelas forças em relação ao ponto O .
Determine o momento da força em relação ao ponto O .
Determine o momento da força em relação ao ponto O .
Dois homens exercem forças de F = 400N e P = 250N sobre as cordas. Determine o momento de cada força em relação a A . Em que sentido o poste girará, horário ou anti-horário?
Se o homem em B exerce uma força P = 150N sobre sua corda, determine a intensidade da força F que o homem em C precisa exercer para impedir que o poste gire; ou seja, para que o momento resultante em