Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 94
Se a tensão de apoio admissível para o material sob os apoios em e for , determine os tamanhos das chapas de apoio quadradas exigidos para suportar a carga. Considere . A dimensão das chapas deverá ter aproximação de . As reações nos apoios são verticais.
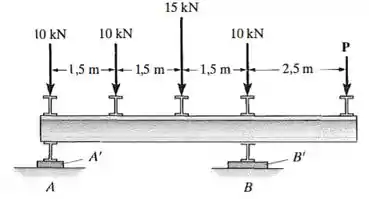
Passo 1
E aí meu povo, como é que vocês estão? Tudo pronto pra mais uma resolução marotinha? Espero que sim, sem mais delongas...
Desenhando as reações a gente tem:
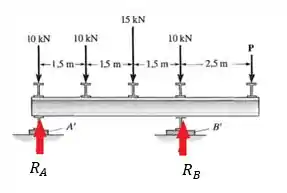
Bacana, agora vamos fazer o somatório dos momentos em no ponto , pois assim a reação no ponto some dos cálculos e a gente consegue encontrar a reação :
Com P = 7,5kN e considerando o sentido anti-horário como positivo, temos:
Para achar , faremos o somatório das forças:
Agora que sabemos as reações nesses pontos, só precisamos calcular a área das chapas para termos a nossa tensão média!
Lembrando-se que as chapas da base são quadradas e portanto sua área será dada por
Passo 2
Até agora a gente calculou reação de apoio e agora que vem a nossa relação com a área da base em A’:
Colocando a área de A em evidência:
(Como eu usei para a força, e para a tensão, a unidade de medida de comprimento que vamos obter é o . Fica a dica!)
Arredondando para um múltiplo de 10mm como é indicado no enunciado, vamos ter
Agora meu pequeno gafanhoto vamos fazer a mesma análise para obtendo assim
Arredondando para um múltiplo de 10mm como indica o enunciado, vamos ter
Pronto, tá finalizado mais um exercício.