Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 31
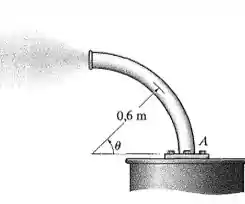
O raio original do tubo curvado é . Se ele sofrer aquecimento não uniforme que provoque uma deformação normal ao longo de seu comprimento , determine o aumento no comprimento do tubo.
Passo 1
Primeiro, vamos representar a situação:
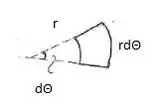
Logo:
Integrando os dois lados:
Resposta
Exercícios de Livros Relacionados
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 1 = - 57,5 × 10 - 6m m / m m ε 2 = - 57,5 × 10 - 6m m / m m ε 4
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 1 = - 93,1μ ε 2 = - 385μ ε 3 = + 210μ Determinar: (a) as três de
As deformações específicas normais determinadas com o uso da roseta da figura, colada na superfície de um componente estrutural, são: ε 2 = - 90 × 10 - 6m m / m m ε 3 = - 190 × 10 - 6m m / m m ε 4 = -
O estado plano de tensões mostrado é conhecido na superfície de um componente de máquina, feito de aço de alta resistência. Sabendo-se que E = 200G P a e G = 80 G P a , determinar a orientação e a int
Para a barra do Prob. 6.146, determinar a leitura que poderia ser obtida para vários carregamentos, se o extensômetro estivesse localizado em um ponto diretamente acima, distante 25m m do ponto C , e