Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 74
A área da seção transversal da barra é . Se ela estiver sujeita a uma carga axial distribuída uniformemente ao longo de seu comprimento e a duas cargas concentradas como mostra a figura, determine a tensão normal média na barra em função de x para .
Passo 1
Falaa!
Queremos determinar a tensão normal média na barra mostrada na figura e para isso devemos lembrar, primeiramente, como se calcula a tensão normal que é dada pela seguinte fórmula
Com
P: resultante da força normal;
A: Área da seção transversal, que ele já dá:
Agora respira, não se assusta com essa carga distribuída nem que a resposta tem que ser em função de . Estamos juntos nessa, vamos arrasar!
A ideia é que a resultante da força normal pode ter um outro nome. Ela pode ser a carga interna normal na seção.
Pera, lembra do que a gente fazia para achar os esforços internos? A gente cortava nossa viga na seção que ele queria, olhava só para o lado que temos informações e achava .
Então é isso que vamos fazer aqui. Vamos usar nossas táticas de achar esforços internos para achar e aplicar na fórmulinha. Bora!
Passo 2
Não temos muitas informações sobre o lado esquerdo da viga, certo? Falta as reações. Então vamos olhar para direita da viga.
Mas onde está nossa seção? Cara, como ele quer em função de , nossa seção está a uma distância genérica da extremidade esquerda (o referencial que ele coloca na figura).
No entanto, para esse caso, como nosso está no intervalo , nossa seção genérica precisa estar nesse intervalo. Logo, não aparece a força de que está aplicada antes à esquerda desse intervalo.
Desenhando, (e esquecendo dessa força de e da parte da carga distribuída que não está na nossa seção, como se a gente tivesse jogado fora essa parte da esquerda) temos algo assim:
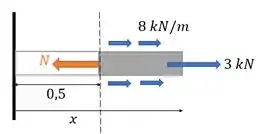
Passo 3
Aí nós usamos a equação de equilíbrio para achar , como a gente fazia quando queria esforços internos.
Na horizontal teremos uma força de reação indo da direita para a esquerda, a qual chamaremos de . Assim, fazendo o somatório das forças nessa direção vamos obter
Por fim, nossa tensão média será dada por