Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 93
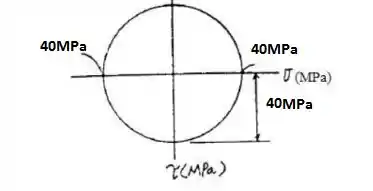
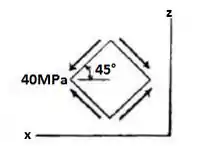
As tensões principais que agem em um ponto em um corpo são mostradas na figura. Desenhe os três círculos de Mohr que descrevem esse estado de tensão e determine as tensões de cisalhamento máximas no plano e as tensões normais médias associadas para os pontos x-y, y-z e x-z. Para cada caso, mostre os resultados no elemento orientado na direção adequada.
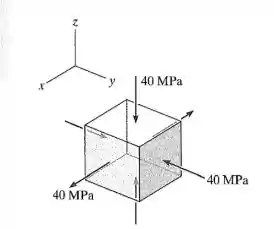
Passo 1
Primeiro, vamos pegar o plano x-y. Sabemos que:
O elemento será orientado da seguinte maneira:
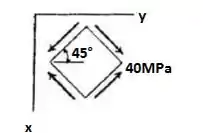
Agora, vamos pegar o plano y-z:
O elemento será orientado da seguinte maneira:
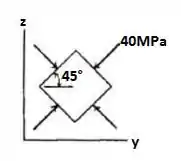
Por fim, vamos pegar o plano x-z:
O elemento será orientado da seguinte maneira:
Passo 2
Agora, devemos fazer o círculo de Mohr:
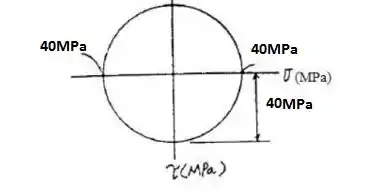
Resposta
Exercícios de Livros Relacionados
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.