Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 105
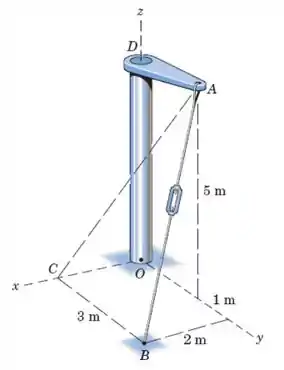
O tensionador é apertado até que a força trativa no cabo valha . Determine a expressão vetorial para a força trativa , como uma força atuando no elemento . Ache também o módulo da projeção de ao longo da linha .
Passo 1
Para encontrar a expressão vetorial para a força , primeiro precisamos encontrar um vetor unitário na direção :Uma dica galerinha, para achar os valores cuidem onde o eixo é “espelhado” (lado oposto), exemplo para o ponto B: o eixo espelha em um comprimento de (notem que está do lado oposto) e sim para outras coordenadas deste ponto e do ponto . Então teremos...
Agora, colocando de forma vetorial teremos
E agora para encontrar o vetor unitário é só dividir pelo próprio módulo
Dessa forma, teremos
Passo 2
E como a força tem módulo (fornecida e aponta na direção de
Passo 3
Agora, queremos projetar na linha , mas para isso precisamos escrever um vetor nessa direção. Vamos fazer algo muito parecido com o que fizemos para direção : please! Não esqueçam, olhem os valores projetados, como mencionado no passo 1
E encontramos o vetor unitário fazendo
E para encontrar a projeção de em é só fazer o seguinte produto escalar
Essa projeção é a que desejamos encontrar. Ufaaaaaaaaaaaaaaa, vencemos