Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 102
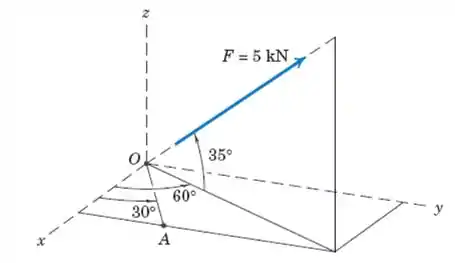
Expresse uma força de como um vetor em termos dos vetores unitários . Determine as projeções entre e o eixo e a linha
Passo 1
E aí meus queridos, tudo bem com vocês? Preparados pra mais uma questãozinha?
Prestem bastante atenção que essa questão é relativamente rapidinha, porém, precisa de um pouco da nossa atenção para que a gente não se perca no meio do caminho. Primeiro de tudo vamos observar a figura do livro que vai nos ensinar como decompor nosso vetor em relação aos eixos
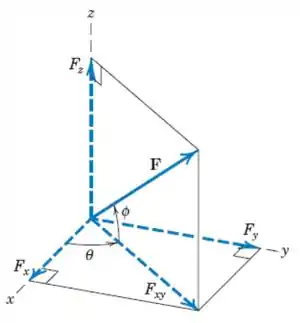
No caso do nosso problema nós conhecemos os ângulos , então, podemos escrever nossos componentes como sendo
Então, projetando a componente horizontal nos componentes e vamos ter
Passo 2
Bom, com isso em mãos podemos fazer a seguinte decomposição
Adotando teremos
Substituindo os valores numéricos vamos ter
Sendo assim, nossa projeção em relação ao eixo será dada por e sobre a linha utilizando a mesma ideia teremos
Cuja componente em vai ser . Pronto, tá resolvido nosso problema.