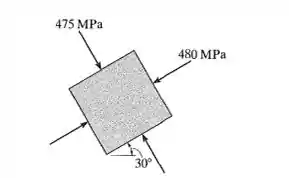
As tensões principais de deformação no plano que agem sobre um elemento são mostradas. Se o material for aço-máquina com tensão de escoamento determine o fator de segurança para escoamento usando a teoria da energia de distorção máxima.
Passo 1
Primeiramente, sabemos que:
Logo, podemos utilizar a equação:
Substituindo, teremos:
Passo 2
Logo, podemos determinar o fator de segurança, que será dado por: