Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas de Revisão - Ex. 127

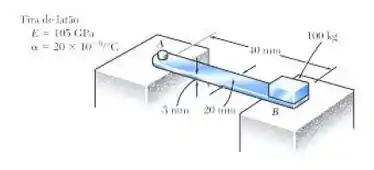
A tira de latão AB foi presa a um suporte fixo em A e apoia-se sobre um suporte rugoso em B. Sabendo que o coeficiente de atrito é 0,60 entre a tira de latão e o suporte B, determine o decréscimo na temperatura para o qual o deslizamento estará na iminência de ocorrer.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine o decréscimo na temperatura para o qual o deslizamento estará na iminência de ocorrer, para isso vamos esboçar o diagrama de corpo livre 😉

Trazendo os dados do enunciado temos: E = 105   G P a   e     α = 20   x   10 - 6 / ° C

Agora vamos calcular o somatório de forcas em Y e X respectivamente

+ ↑ ∑ F y = 0 :       N - W = 0       N = W → + ∑ F x = 0 :           P - μ N = 0       P = μ W = μ m g

A deformação temos: δ = - P L E A + L α   x   ∆ T = 0         ∆ T = P E A α = μ m g E A α

Sabendo que: μ = 0,60 ,   m = 100   k g ,   g = 9,81 m s 2 ,   E = 105   x   10 9 P a

Calculando a área temos:

A = 20   x   3 = 60   m m 2 = 60   x   10 - 6 m 2 ∆ T = 0,60   x   100   x   ( 9,81 ) 105   x   10 9   x   60   x   10 - 6   x   ( 20   x   10 6 )  

Resposta

∆ T = 4,67 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga e o carregamento mostrados, determine a declividade do ponto A . Use E = 200G P a .
Para a viga e o carregamento mostrados, determine a deflexão do ponto C . Use E = 200G P a .
Para a viga e o carregamento mostrados, determine a inclinação na extremidade A . Use E = 200G P a .
Para a treliça e o carregamento mostrados, determine a deflexão vertical e horizontal do nó C .
Para a treliça e o carregamento mostrado, determinar a energia de deformação