Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas - Ex. 95
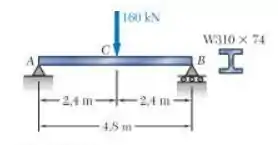
Para a viga e o carregamento mostrados, determine a inclinação na extremidade . Use .
Passo 1
Fala aí, gurizada. Tudo beleza? Bora fazer mais um exercício pra ficar craque.
Nesta questão, temos que determinar a inclinação no ponto . Portanto, vamos adicionar uma carga fictícia na extremidade Bora esboçar o pra ver isso:
Em seguida, vamos utilizar as equações de equilíbrio para determinar as reações de apoios:
Com isso, vamos determinar o momento fletor para cada porção da viga. Para a primeira, compreendida no intervalo , o momento é dado por:
E a sua derivada em relação a , ou seja, a sua inclinação vai ser:
Para a outra porção da viga, ou seja, a porção compreendida em , temos que o momento fletor vai ser:
E a inclinação, dada pela derivada parcial em , vai ser:
Passo 2
Em seguida, vamos determinar a energia de deformação total para esta viga. Vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, ela vai ser a soma das energias de deformação para cada porção da viga. Fica assim:
Onde os limites de integração correspondem ao comprimento de cada segmento. Em seguida, vamos derivar esta equação dos dois lados em função de . Assim, obteremos a inclinação que, neste caso, vai ser no ponto , temos:
Substituindo:
Para este perfil de viga, o momento de inercia é tabelado e pode ser encontrado na internet ou nos livros. Ele é dado por:
Substituindo na equação:
Vamos resolver esta integral pra você para adiantarmos o processo. Assim, a deformação em vai ser:
Isso é tudo, pessoal. Bora zerar esse livro.