Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 5.Problemas - Ex. 49
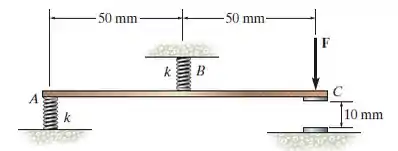
Uma tira de metal rígida, com peso desprezível, é usada como parte da chave eletromagnética. Se a rigidez das molas em e for e a tira estiver originalmente horizontal quando as molas estiverem não esticadas, determine a menor força necessária para fechar a lacuna do contato em .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta questão é bem semelhante a questão em termos de geometria e forças. Nesta questão, queremos saber a força mínima para que o ponto se desloque 10 cm para baixo.
Desta forma será, fundamental fazermos um diagrama de corpo livre identificando as forças aos quais estão submetidos!!! Então, o nosso diagrama de equilíbrio será:
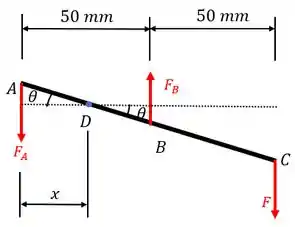
Devido a geometria, existe um ponto entre os pontos e que não se desloca.
Agora que já identificamos todas as reações, basta lembrarmos das relações de equilíbrio
Então, vamos as contas!
Passo 2
Vamos começar identificando a relação entre as forças. Fazendo o somatório em relação ao ponto , teremos:
Já o somatório em relação ao ponto , teremos:
E assim nós identificamos as relações entre as forças!
Passo 3
Mas quem é a força ? Este é o objetivo da questão e nada descobrimos até agora!
Vamos com calma. Agora vamos ter que fazer uma análise da geometria, para saber o quanto se deforma cada mola.
Então, pela geometria do problema, temos a seguinte relação entre os triângulos (a direita e a esquerda do ponto ):
Só que . Portanto,
Bom, temos duas equações e três incógnitas (, e ). Precisamos de mais uma equação para poder resolver o nosso problema.
Esta equação vem exatamente da relação da rigidez das molas. Como elas são iguais, temos:
Só que e . Portanto,
E agora já temos todas as informações necessárias para dar prosseguimento com a questão!
Passo 4
Como temos agora três equações com três incógnitas, basta resolvermos o sistema. Assim, vamos começar determinando a distância . Ela será:
Com este valor, voltamos para calcular , que será:
Portanto, a força é:
E assim finalizamos a questão!