Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 139

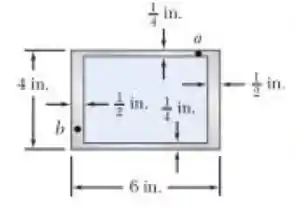
Um torque T de 5   k i p * pés é aplicado a um eixo de alumínio de seção vazada com sua seção transversal mostrada na figura. Desprezando o efeito da concentração de tensões, determine a tensão de cisalhamento nos pontos a e b.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede para que a gente determine a tensão de cisalhamento nos pontos a e b. Primeiramente temos que calcular o torque, vem comigo :D

T = 5   x   10 3   x   12 = 60   x   10 3   l b * i n .

Área delimitada pela linha central, vejam a imagem abaixo :D

a = b h = 5,5   x   3,75 = 20,625   i n ²

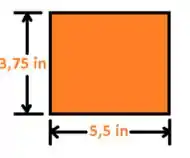
Agora podemos determinar a tensão de cisalhamento considerando a espessura de: t = 0,25   i n .

τ = T 2 t a = 60   x   10 3 2   x   0,25   x 20,625 5,82   x   10 3   p s i

No ponto b, t = 0,50   i n . τ = T 2 t a = 60   x   10 3 2   x   0,50   x 20,625 = 2,91   x 10 3   p s i  

Resposta

τ = 5,82   k s i τ = 2,91   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo maciço está preso ao suporte em C e sujeito aos carregamentos de torção mostrados. Determine a tensão de cisalhamento nos pontos A e B e faça um rascunho da tensão de cisalhamento nos elementos
A haste tem diâmetro de 12mm e peso de 80N/m . Determine a tensão de torção máxima provocada na haste pelo seu peso em uma seção localizada em A .
Resolve o Problema 5.24 para a tensão de torção máxima em B .
Ao perfurar um poço a velocidade angular constante, a extremidade inferior do tubo de perfuração encontra uma resistência à torção T A . Além disso, o solo ao longo das laterais do tubo cria um torque
Os eixos de aço estão interligados por um filete de solda como mostra a figura. Determine a tensão de cisalhamento média na solda ao longo da seção a - a se o torque aplicado aos eixos for T = 60Nm .