Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 24

A haste tem diâmetro de 12   mm e peso de 80   N/m . Determine a tensão de torção máxima provocada na haste pelo seu peso em uma seção localizada em A .

Passo 1

A haste de peso 80   N/m (distribuído!) está preso a uma parede. Queremos a tensão máxima de torção τ M na seção A .

Vamos precisar da fórmula da torção:

τ = T   r J

Essa tensão é máxima nas bordas do eixo. Como o diâmetro é 12   mm , então r = 6   mm e o momento polar de inércia fica:

J = π r 4 2 = 2035,752   mm 4

Só nos falta achar o torque T A que ocorre na seção A !

Passo 2

O peso distribuído da haste vai puxá-la para baixo. Vamos ver que torque isso gera para seção A . Fique atento: queremos os torques que giram ao redor do eixo preso na parede (o eixo A B ).

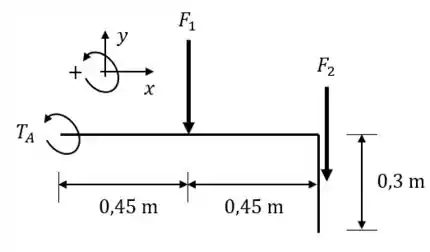
O peso do eixo horizontal vai atuar no centro de massa dele (a 0,45   m do eixo A B ) e será

F 1 =   80   N/m ⋅ 0,9   m = 72   N

Já o peso do eixo vertical vai atuar a 0,9   m do eixo A B e com intensidade

F 2 =   80   N/m ⋅ 0 , 3   m = 24   N

Fazendo equilíbrio de momentos para A

∑ M A = 0       →         T A - 0,45   m ⋅ F 1 - 0,9   m ⋅ F 2 = 0

T A = 54   Nm

Passo 3

Só aplicar a fórmula da torção agora para acabar.

τ = T   r J       →         τ M = 54   Nm ⋅ 6   mm 2035,752   mm 4

τ M = 159,155   MPa

Resposta

Tensão máxima de torção: τ M = 159,155   MPa .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um torque de intensidade T = 120N ⋅ m é aplicado ao eixo A B do trem de engrenagens mostrado. Sabendo-se que a tensão admissível de cisalhamento é de 75M P a , nos três eixos maciços, determinar o diâ
O eixo maciço A B é feito de um aço, com uma tensão admissível ao cisalhamento de 80M P a e o tubo C D é feito de latão, com uma tensão admissível ao cisalhamento de 50M P a . Determinar: (a) o maior
O eixo A B é feito de um aço com tensão admissível ao cisalhamento de 90M P a , e o eixo B C é feito de uma liga de alumínio com tensão admissível de cisalhamento de 60M P a . Sabendo-se que o diâmetr
O eixo maciço A B tem um diâmetro d s = 38m m e é feito de aço, com uma tensão admissível ao cisalhamento de 80M P a , enquanto que o tubo C D é feito de latão, com uma tensão admissível ao cisalhamen
Um torque de intensidade T = 10 0N ⋅ m é aplicado ao eixo A B do trem de engrenagens mostrado. Sabendo-se que os diâmetros dos três eixos maciços são, respectivamente, d A B = 21m m , d C D = 30m m e