Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 58

Um colar de tem uma velocidade , quando ele se com uma pequena placa presa na extremidade da barra , de diâmetro . Usando-se , determinar:

a carga estática equivalente para a barra;

a máxima tensão na barra;

a máxima deflexão na extremidade .

Passo 1

Faaala, queridas e queridos! Como anda a vida?

Bora resolver um exercício de carregamento axial produzido por impacto?

Essa questão quer saber três informações diferentes. Primeiro, ela quer que a gente determine a força que produziria a mesma tensão e deformação na barra que o choque. O enunciado chama essa força de carga estática. A carga estática axial aplicada em uma barra pode ser calculada reorganizando a equação 10.14 do livro.

onde é a energia que a barra absorve através do impacto do colar .

Depois a barra quer que a gente calcule a máxima tensão na barra. Fazemos isso, dividindo pela área da seção transversal da barra.

Por fim, o exercício quer que a gente determine a máxima deflexão na barra extremidade da barra.

Esse valor é obtido, se a gente lembrar que a energia vale:

A figura abaixo mostra os dados que temos para tudo isso.

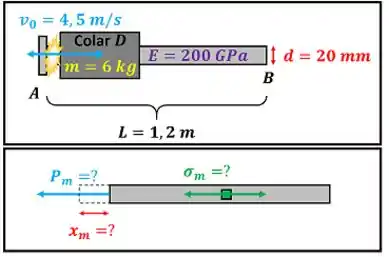
Agora que entendemos o que precisamos calcular, vamos começar a resolver o exercício no próximo passo.

Passo 2

Vamos começar os cálculos pela carga estática . Essa carga estática deve ser calculada a partir da equação 10.14 do livro que depende da energia absorvida pela barra e causada por uma força axial . No entanto, não sabemos quanto vale . Para determinar , vamos supor que a barra absorve toda a energia cinética do colar . Logo, vale.

onde é a massa do colar e é a velocidade do colar.

Além disso, a equação de tem outro termo que ainda não conhecemos. O termo ! Ele é a área da seção transversal da barra. Como a barra é circular, usamos o diâmetro para calcular . Mas cuidado! Temos que nos lembrar de passar o diâmetro de para antes da conta!