Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas Revisão - Ex. 141
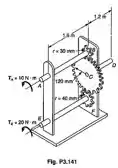
Três eixos maciços de aço , cada um com 18 mm de diâmetro, são conectados pelas engrenagens mostradas. Para os carregamentos dados, determinar: (a) o ângulo de torção da extremidade A, do eixo AB; (b) o ângulo de torção da extremidade E, do eixo EF
Passo 1
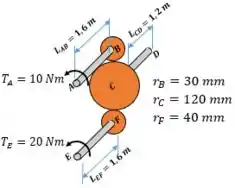
Vamos começar calculando a força que atua na engrenagem C.
Pra começo de conversa, as engrenagens B e F exercem forças sobre a engrenagem C. A força resultante em C gera um torque que atua em no eixo CD.
Primeiro a gente calcula a força em cada engrenagem:
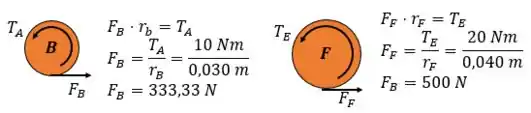
E agora podemos calcular o torque sobre a engrenagem C:
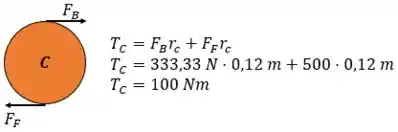
Passo 2
Agora vamos olhar para os eixos.
Todos os três eixos têm o mesmo diâmetro
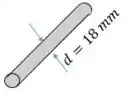
O momento de inércia polar é:
Passo 3
Beleza!
Agora já dá para calcular as torções geradas nas barras. Ou seja, já dá para calcular o ângulo entre as extremidades de uma mesma barra.
Primeiro vamos calcular o ângulo relativo entre o ponto A e B:
O ângulo relativo entre os pontos E e F:
E o ângulo relativo entre os pontos C e D:
Passo 4
Como o ponto D não sofre nenhum esforço, podemos usar o ponto D como um ponto fixo. Assim, o ângulo do ponto C será igual a deformação da barra:
Agora podemos usar as relações de engrenagens para determinar a deformação dos pontos B e F:
Para o ponto B:
Para o ponto F:
Passo 5
Agora está tudo certo!
Podemos calcular as deformações absolutas no ponto A:
E para o ponto E: