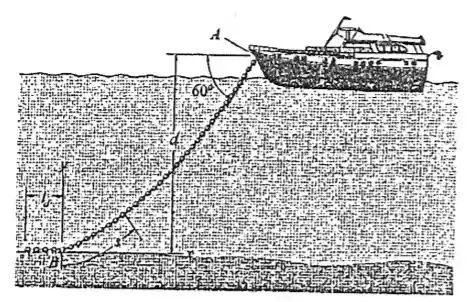
O iate está ancorado com uma corrente que tem uma extensão total de, uma massa por unidade de comprimento de , e a tração na corrente em é . Determine o comprimento da corrente que encosta no fundo do mar. Qual é a distância ? Suponha que os efeitos de flutuação da água sobre a corrente sejam desprezíveis. Dica: Estabeleça a origem do sistema de coordenadas em , conforme mostramos, a fim de encontrar o comprimento da corrente .

Desejamos encontrar o valor de e . Para isso vamos fazer o seguinte:

Que é a componente horizontal da força em. Para descobrirmos o valor de algumas constantes que nos serão importantes para acharmos o valor de vamos utilizar a seguinte equação

Além disso, para . Então, vamos ter apenas

Podemos fazer ainda

Substituindo e integrando vamos obter

Quando

A inclinação do cabo em é

Usando a equação vamos ter

O comprimento da corrente vai ser, então,

Utilizando o valor de na equação vamos obter

Dessa forma teremos