Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 112
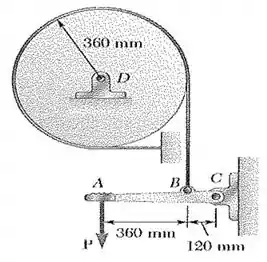
112. Um freio de cinta é utilizado para controlar a velocidade de um volante, conforme mostra a figura. Os coeficientes de atrito são e . Determine a intensidade do torque que deve ser aplicado ao volante, sabendo que , e que o volante está girando no sentido anti-horário em velocidade constante.
Passo 1
Bom! Vamos lá para mais um probleminha sobre atrito. Sendo assim, qual é a primeira coisa que temos que fazer?
Ora bolas! Já tá meio que repetitivo, mas é o procedimento padrão; tá? Temos que fazer o diagrama de corpo livre para o nossos sisteminha. Vamos lá! Façamos primeiro, o diagrama para o volante:
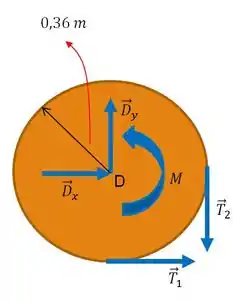
Essa representação de e , advém do fato de que se o clilindro estiver rolando no sentido anti-horário, o deslizamento da freia em relação ao clindro é no sentido horário.
Voltando ao que interessa, vamos tratar de descobrir o quanto valem e . Para isso, façamos também o diagrama de corpo livre para a alavanca :
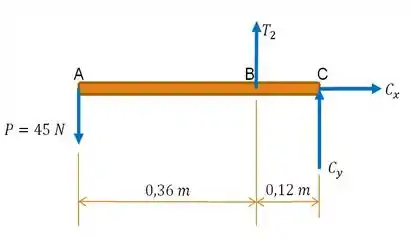
Bom! Com isso, já fica mais fácil obter o valor de uma das forças, no caso, . Para fazer isso, devemos realizar o somatório dos momentos com relação a um ponto de interesse. Que tal o ponto ?
Passo 2
E agora que já obtemos o valor de , bora utilizar a velha relação que conhecemos para o atrito na condição em que como podemos ver no enunciado, ocorre deslizamento:
Onde , dessa vez, vai ser a tração máxima e vai ser a tração mínima. E olho lá no valor do coeficiente de atrito que iremos usar. Estamos trabalhando com a condição de deslizamento. Logo, peguemos , igual a . E o ângulo , que é o ângulo subentendido pelo arco do tambor sobre a qual a correia está enrolada, ao olhar a figura do enunciado percebemos que vale ou radianos. Sendo assim, obtemos que:
Passo 3
Agora, que já sabemos o quanto valem as nossas forças, para achar a intensidade do torque que deve ser aplicado ao volante, basta simplesmente aplicar o somatório dos momentos em relação ao ponto: