Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 1

Um trator de é usado para erguer de cascalho. Determine a reação em cada uma das duas (a) rodas traseiras A, (b) rodas dianteiras B.

Figura P4.1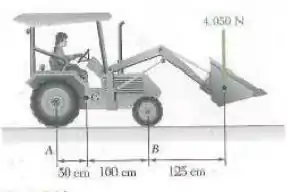

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Precisamos determinar a reação em cada uma das rodas do trator. Chamaremos a reação em cada uma das rodas traseiras de e a das rodas dianteiras de .

Olhando para a imagem do enunciado, podemos notar que todas as forças estão em (Newtons) e todas as medidas estão em cm (centímetros). Portanto, não precisaremos converter unidades e as reações serão encontradas em .

Passo 2

Agora consideraremos o seguinte diagrama de corpo livre para o trator:

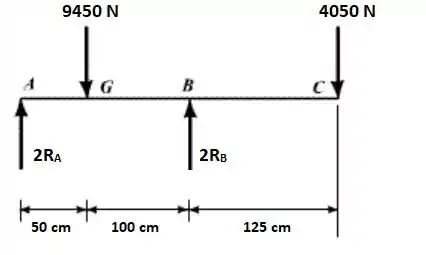
Como temos duas rodas dianteiras e duas rodas traseiras. As forças nos pontos A e B são representadas com 2 e 2 . Sendo e as forças em uma roda traseira e em uma roda dianteira, respectivamente.

Analisando o diagrama podemos fazer o somatório dos momentos em torno de A ():

indica a reação em cada uma das rodas dianteiras. Observe que o sinal foi positivo, o que indica que a direção da resultante é para cima, assim como representado no diagrama de corpo livre.

Passo 3

Faremos agora o somatório de forças na vertical para determinar o valor da reação em cada uma das rodas traseiras:

Substituindo o valor de

indica a reação em cada uma das rodas traseiras. Observe que o sinal foi positivo, o que indica que a direção da resultante é para cima, assim como representado no diagrama de corpo livre.