Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 4

Para a viga e carregamento mostrados na figura, determine (a) a reação em A, (b) a tração no cabo BC.

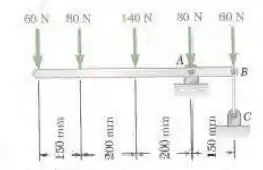
Figura P4.4

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Precisamos determinar a reação em A e a tração no cabo BC (. Sabe-se, pelo princípio da ação e reação, que a tração que a viga exerce no cabo BC é a mesma força que o cabo exerce sobre a viga. Assim podemos encontrar a tração no cabo BC por uma análise de equilíbrio da viga.

Olhando para a imagem do enunciado, podemos notar que todas as forças estão em (Newtons) e todas as distâncias estão representadas em mm (milímetros). Portanto, não será necessário converter unidades.

Passo 2

Agora teremos o seguinte diagrama de corpo livre:

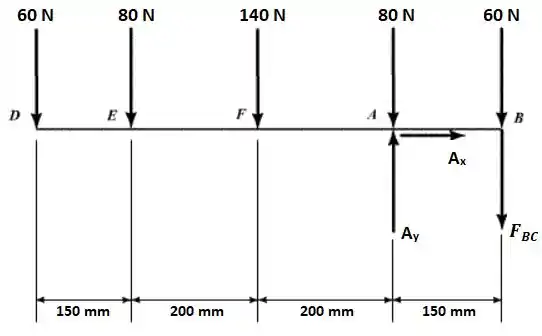
Observe que em A podem existir reações na direção (horizontal) e na direção (vertical), enquanto em B a única reação é na vertical, devido a natureza de força de tração no cabo BC.

Analisando o diagrama podemos fazer o somatório dos momentos em torno de B para determinar a componente .

Observe que o sinal foi positivo, o que indica que a direção da componente é para cima, assim como representado no diagrama de corpo livre.

Passo 3

Analisando agora as forças horizontais podemos determinar a componente , aplicando o somatório das forças nessa direção:

Com as duas componentes da força determinadas e sabendo que a componente horizontal é nula. Concluimos que:

indica a reação no ponto A que está orientada na vertical e direcionada para cima.

Passo 4

Aplicaremos agora o somatório das forças na vertical (direção y) para determinar a reação em B, que conforme explicado anteriormente é igual à tração no cabo BC (.

indica a reação em B e também no cabo BC, o valor positivo mostra que na viga ela está orientada conforme o diagrama de corpo livre utilizado, portanto para baixo. Pelo princípio da ação e reação , no outro elemento (cabo BC) a orientação é contrária, portanto, para cima, tracionando o cabo.