Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 62
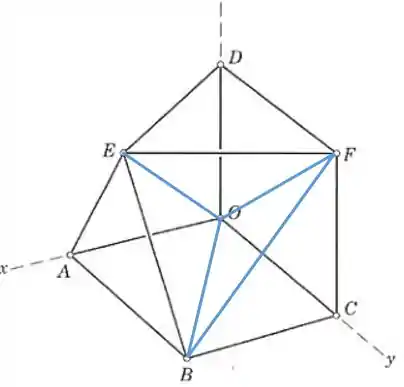
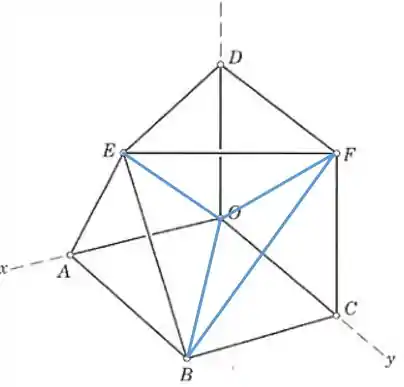
Uma treliça espacial está sendo projetada com os elementos mostrados. Quantos elementos adicionais são necessários para tornar a treliça estável internamente? Nomeie os elementos (especificando suas extremidades) que poderiam gerar uma possível configuração de estabilidade interna.
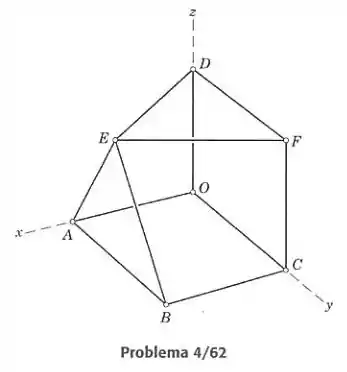
Passo 1
Para uma treliça espacial estaticamente determinada como um todo, se temos nós e elementos, teremos equações de estabilidade (3 equações de força para cada nó) e incógnitas (uma para cada elemento e 6 para forças externas atuando na treliça). Então a treliça deve satisfazer a relação .
Passo 2
Nesse caso, temos e , então temos
Então existem menos elementos do que o necessário para a estabilidade. Devemos adicionar 4 elementos (sem adicionar nós), e esses elementos têm que tornar a treliça uma estrutura rígida. A estrutura fica certamente rígida quando todos os pontos dela pertencem a tetraedros rígidos, então devemos posicionar novos elementos de modo a formar tetraedros.
Passo 3
Primeiro, ligamos e e formamos o tetraedro , e esses 4 pontos estão então fixados.
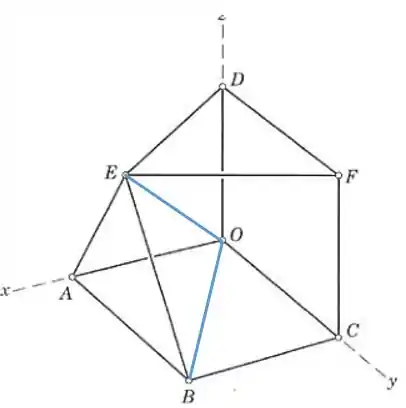
Agora ligamos , criando o tetraedro , fixando então os pontos e :
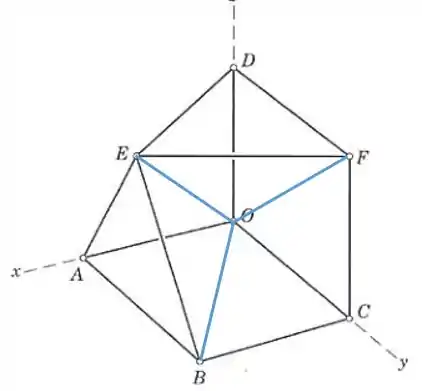
Só falta fixar , e fazemos isso adicionando , criando o tetraedro :
Agora temos
E a estrutura satisfaz a condição de estabilidade.
Resposta
4 elementos adicionados para a estabilidade. , , e .
